SISTEMA DIÉDRICO
AXONOMETRÍAS
Unidad 8
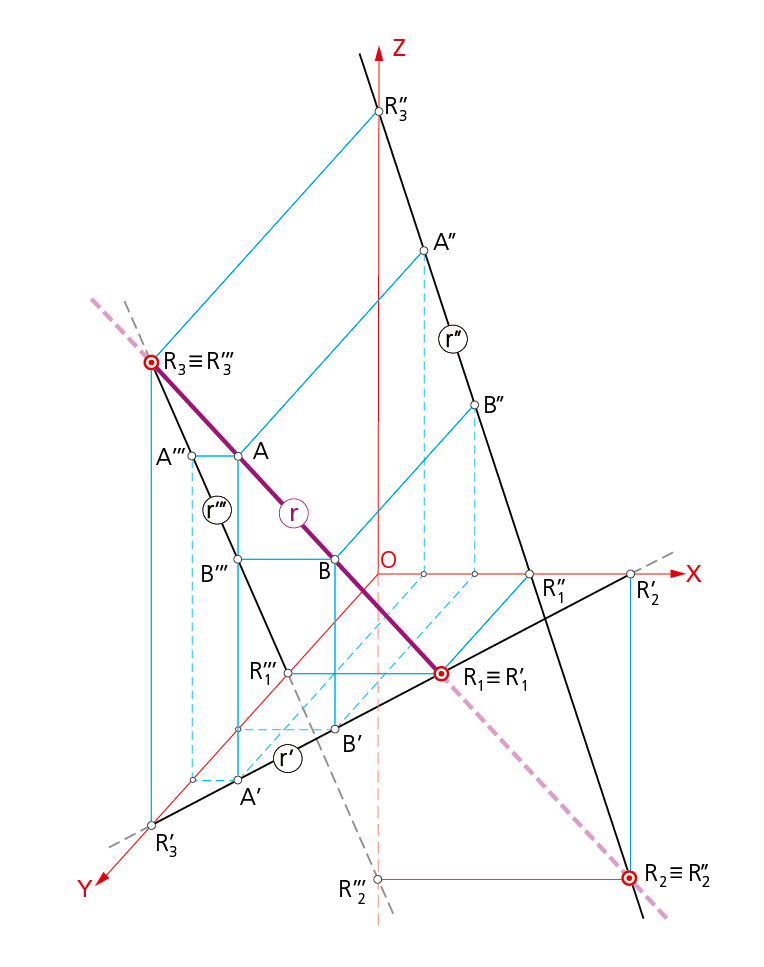
Representación de una recta cualquiera y determinación de sus trazas.
7 - LA RECTA EN AXONOMETRÍA OBLICUA
Como sucede en todos los sistemas perspectivos, en caballera la recta viene definida por su proyección directa r y una de sus proyecciones sobre uno cualquiera de los planos coordenados, o bien, mediante dos de sus proyecciones.
Para que un punto pertenezca a una recta, es necesario que las proyecciones del punto se encuentren en las proyecciones homónimas de la recta, es decir, que A esté en r, A’’ en r’, A’’ en r’’ y A’’’ en r’’’.
Los puntos R1, R2 y R3 resultan ser las trazas de la recta r con los coordenados XY, XZ e YZ respectivamente. Para hallar la traza, por ejemplo, con el plano XY, se busca el corte de la proyección directa r con la proyección r’ sobre dicho plano, obteniendo el punto R1. Si se consideran los puntos de corte R’2 y R’3 de la proyección r’ con los ejes X e Y, y por ellos se trazan paralelas al eje Z, se determinan, por intersección con la perspectiva directa r, los otros dos puntos traza R2 y R3 respectivamente. Obsérvese cómo los puntos traza, tanto en su perspectiva directa como en sus proyecciones homónimas, están alineados.
Sólo se considera vista la parte de recta que se encuentra en el primer octante del espacio, donde se sitúa el observador.
7.1 Tipos de rectas particulares.
Son aquéllas que mantienen alguna relación de pertenencia, paralelismo o perpendicularidad con los coordenados.
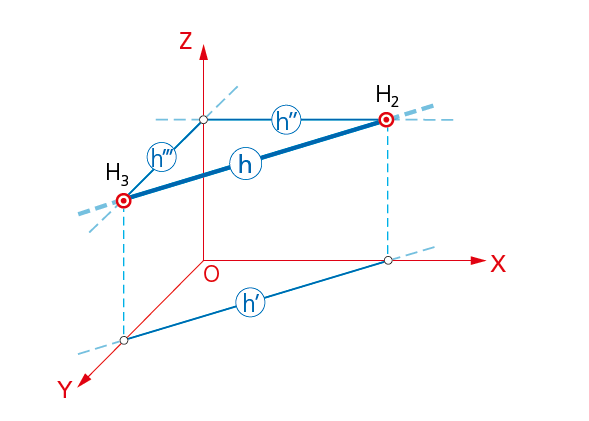
7.1.1. Paralelas a los planos coordenados.
El producto de una traslación por un giro (o viceversa) es un giro cuyo centro se determina como en el caso anterior; ya que una traslación es un giro de centro impropio.
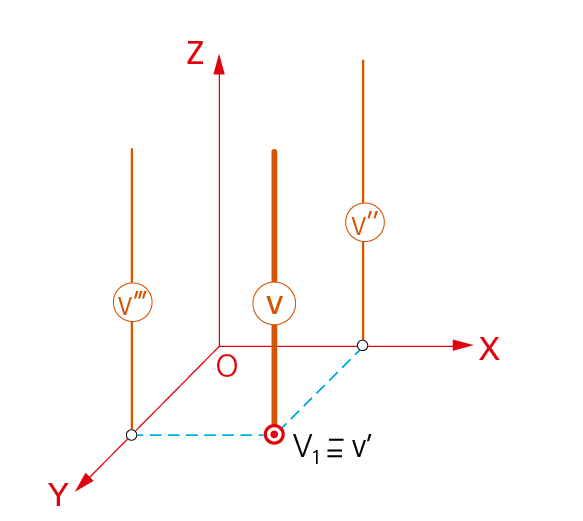
7.1.2. Paralelas a los ejes coordenados.
En la figura, la recta v perpendicular al plano XY (paralela al eje Z), donde su proyección sobre el plano horizontal (XY) es un punto (v’), que además es punto traza horizontal (V1) de dicha recta.
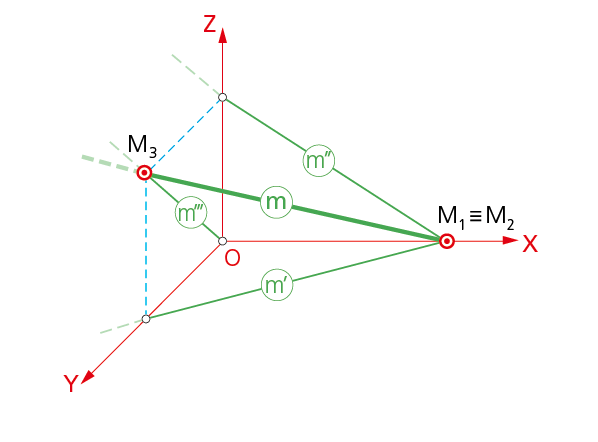
7.1.3. Rectas que cortan a los ejes.
En la figura, la recta m corta al eje X. Las proyecciones m’ y m’’, así como la proyección directa m, se cortan en un mismo punto del eje X (M1=M2) que es, además, punto traza.
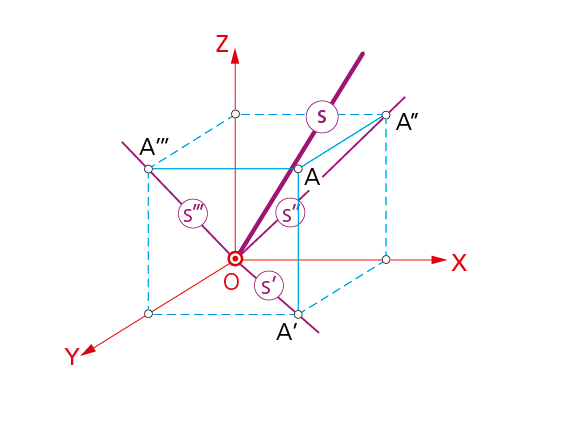
7.1.4. Rectas que pasan por r el origen.
En la figura, la recta s pasa por el origen O, al igual que sus tres proyecciones.