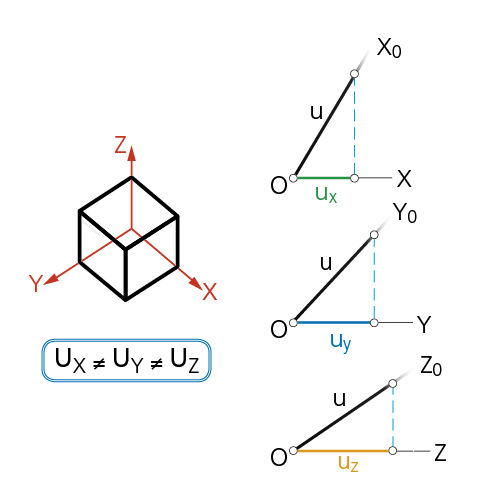SISTEMA DIÉDRICO
AXONOMETRÍAS
Unidad 8
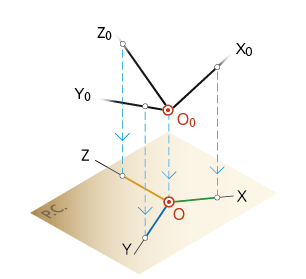
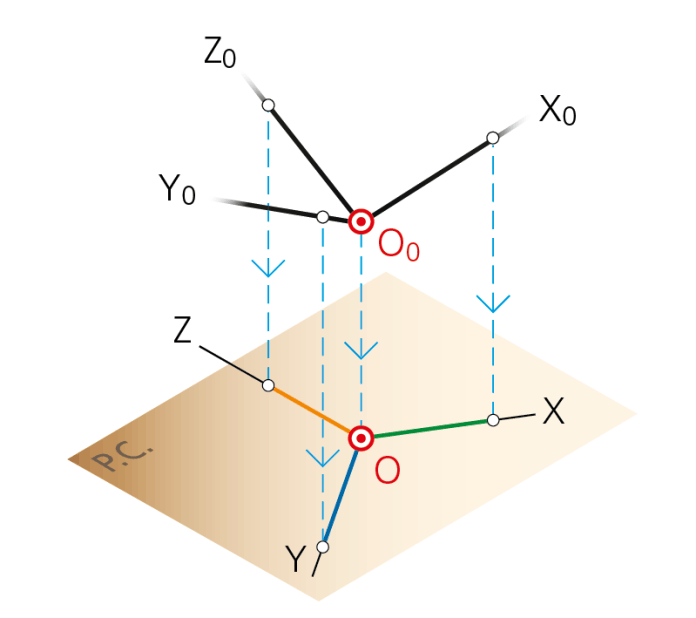
2- AXONOMETRÍAS ORTOGONALES
De las diferentes posiciones entre el plano del cuadro y el triedro trirrectángulo, nacen los tres tipos de perspectivas axonométricas:
2.1 Perspectiva Isométrica
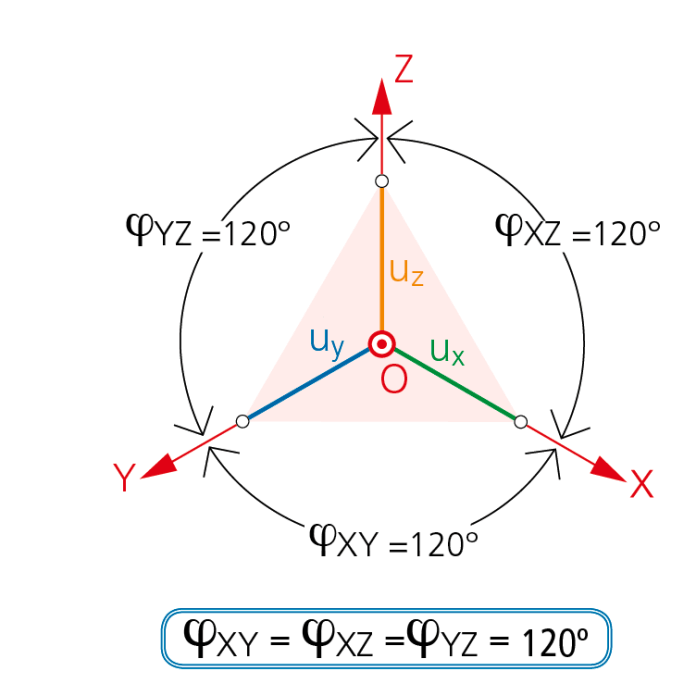
Cuando los ángulos que forman las aristas del triedro trirrectángulo con el plano del cuadro son iguales. Resultando que: ϕXY = ϕYZ = ϕxz = 120° En este caso, las trazas del plano del cuadro forman un triángulo equilátero y, el coeficiente de reducción es igual para los tres ejes coordenados:
√2 / √3 = 0,81649 (en la prática se toma como reducción en cada
eje 0,8 = 4/5).
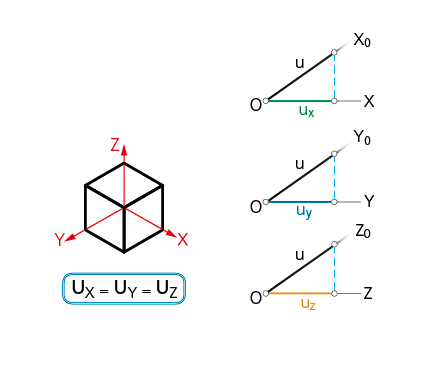
Ejemplo de representación de un hexaedro en isométrica.
2.2 Perspectiva Dimétrica
Cuando dos de los ángulos que forman las aristas del triedro trirrectángulo con el plano del cuadro son iguales.
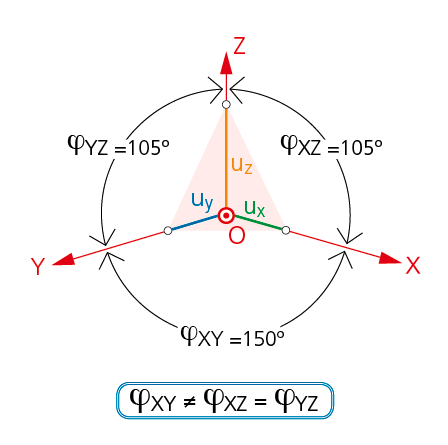
Así, por ejemplo: α = β ≠ γ lo que trae consigo que: ϕXY ≠ ϕYZ = ϕxz
En este caso, las trazas del plano del cuadro determinan un triángulo isósceles y la unidad de medida tendrá igual reducción sobre los dos ejes que delimitan el ángulo desigual. En esta perspectiva el ángulo distinto es el que forma el eje X con el Y, lo que significa que ambos ejes tendrán igual reducción y distinta de la que corresponde al eje Z.
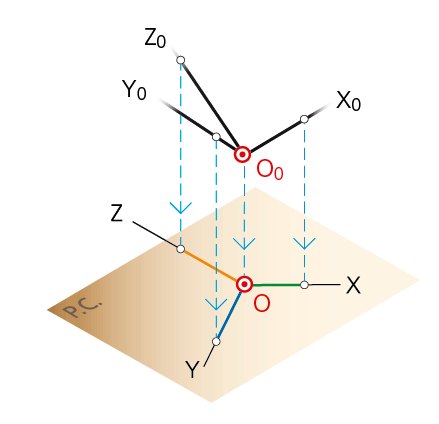
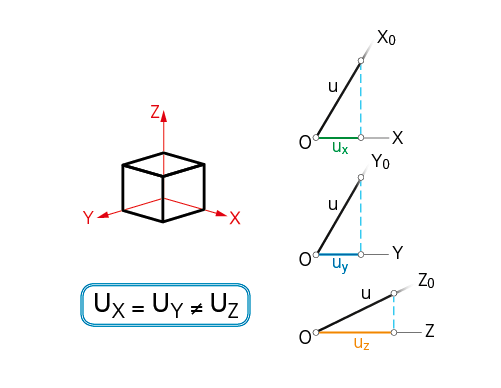
Ejemplo de representación de un hexaedro en dimétrica.
2.3 Perspectiva Trimétrica
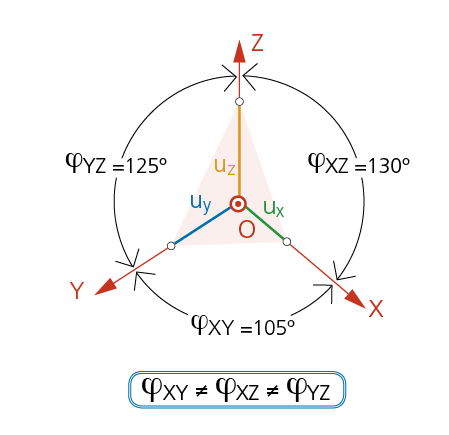
Cuando los tres ángulos son distintos.
Esto es: α ≠ β ≠ γ resultando que: ϕXY ≠ ϕYZ ≠ ϕxz
En este caso, las trazas del cuadro forman un triángulo escaleno; siendo la reducción distinta para cada eje coordenado.