SISTEMA DIÉDRICO
ASONOMETRÍAS
Unidad 8
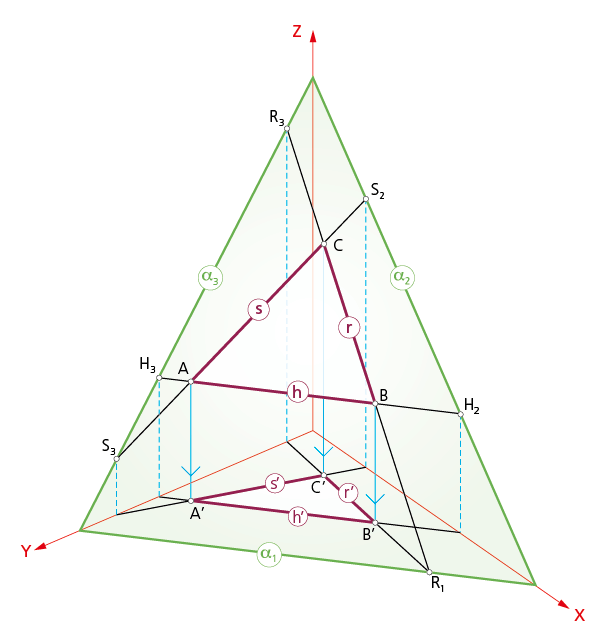
Representación del plano
dado por tres puntos A, B y C.
4• EL PLANO EN AXONOMETRÍA ORTOGONAL
Los planos, como en el sistema diédrico, se representan por sus trazas, es decir, por las rectas de intersección del plano con los coordenados. Como un plano puede venir definido por tres puntos o por dos rectas que se cortan, se hallan los puntos traza de las rectas h, r y s (que pasan por A, B y C). Uniendo puntos traza homónimos se determinan las trazas del plano (α1, α2 y α3). Hay que recordad, como en casos anteriores, que únicamente se considera visto la porción de plano comprendido en el primer triedro.
4.1 Posiciones particulares del plano.
Como más relevantes pueden considerarse las siguientes:
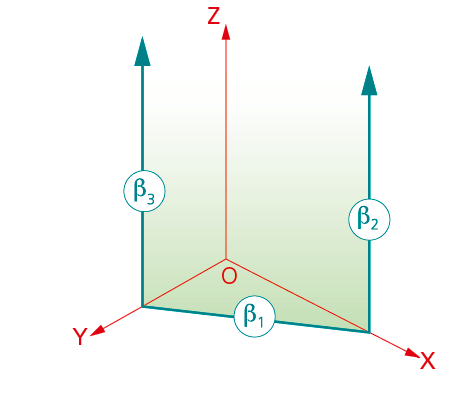
4.1.1. Planos proyectantes.
Planos perpendiculares a los coordenados.
En la figura de la derecha se representa un plano b proyectante horizontal.
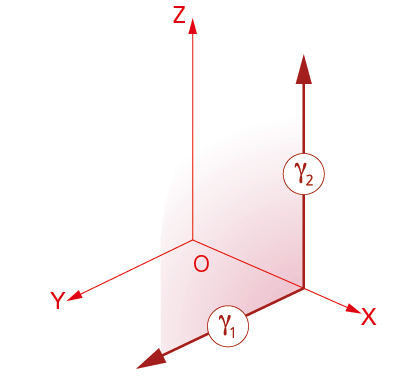
4.1.2. Planos paralelos a los axonométricos.
En la figura a la izquierda de estas líneas podemos ver el plano γ paralelo al coordenado YZ.
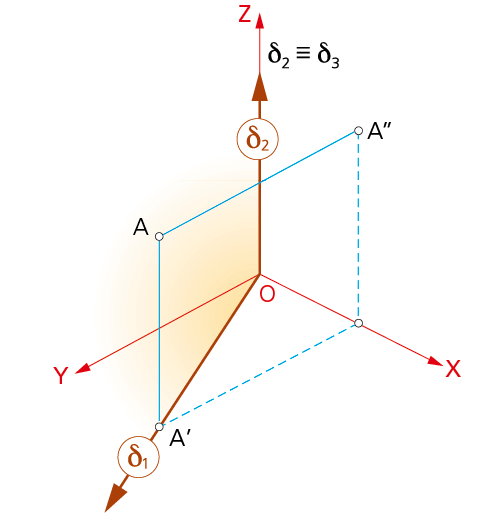
4.1.3. Planos que contienen a los ejes.
En la figura, el plano δ que contiene al eje Z.
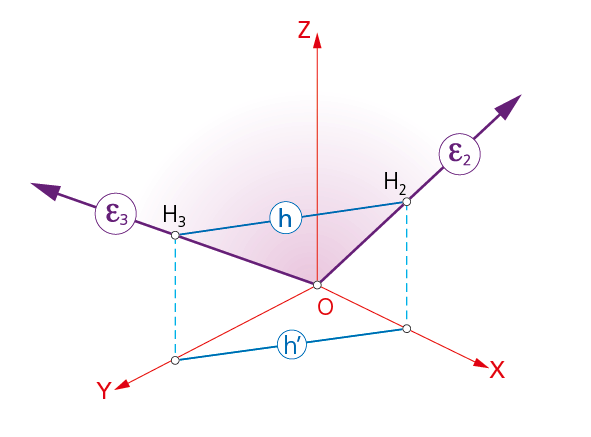
4.1.4. Planos que pasan por el origen.
En la figura, el plano ε que pasa por el origen O.

4.2 Rectas contenidas en un plano.
Una recta pertenece a un plano cuando las trazas de la recta se encuentran sobre las trazas homónimas del plano que la contiene. Asimismo, para que un punto pertenezca a un plano es preciso que dicho punto se encuentre sobre una recta contenida en el plano.
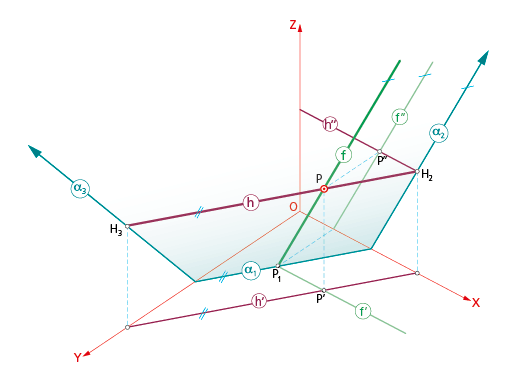
Recta horizontal del plano.
La recta h, contenida en un plano cualquiera α, es paralela al plano horizontal XY. Las proyecciones h (directa) y h’ serán paralelas a la traza α1 del plano y las proyecciones h” y h’” (no dibujadas) serán paralelas a los ejes X e Y respectivamente. Obviamente, no posee traza horizontal (H1).

Recta frontal del plano.
Su vértice es exterior a la circunferencia y sus lados son secantes o tangentes a ella.
Su valor es igual a la semidiferencia de los ángulos centrales que abarcan sus lados.