SISTEMA DIÉDRICO
AXONOMETRÍAS
Unidad 8
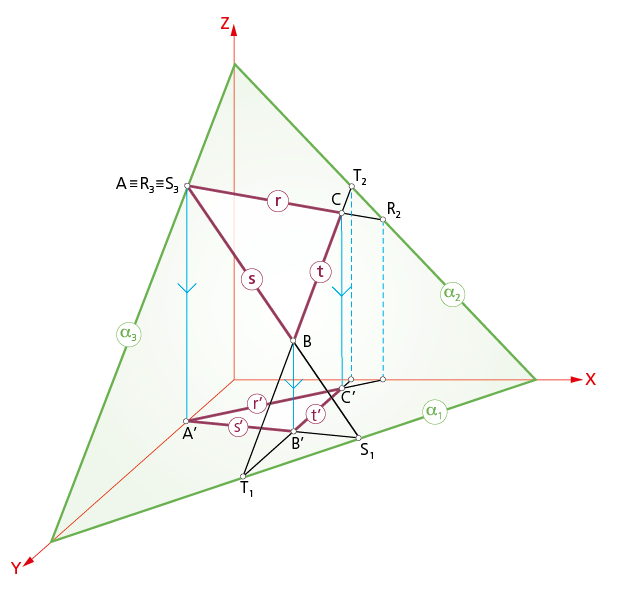
Representación del plano a dado por tres puntos A, B y C que corta a los tres ejes coordenados.
8 - EL PLANO EN AXONOMETRÍA OBLICUA
Los planos, como en anteriores sistemas de representación, pueden representarse mediante sus trazas, es decir, por las rectas de intersección del plano (α1-α2-α3) con los coordenados. Como de costumbre, el plano puede venir dado por tres puntos (A, B y C ) o por dos rectas que se cortan; en cualquier caso, se hallan los puntos traza de las rectas r, s y t que lo definen. La unión de trazas homónimas determina las trazas del plano a dibujar. Únicamente se considera vista la porción de plano comprendida en la parte positiva del triedro fundamental.
8.1 Tipos de planos.
Son aquéllas que mantienen alguna relación de pertenencia, paralelismo o perpendicularidad con los coordenados.
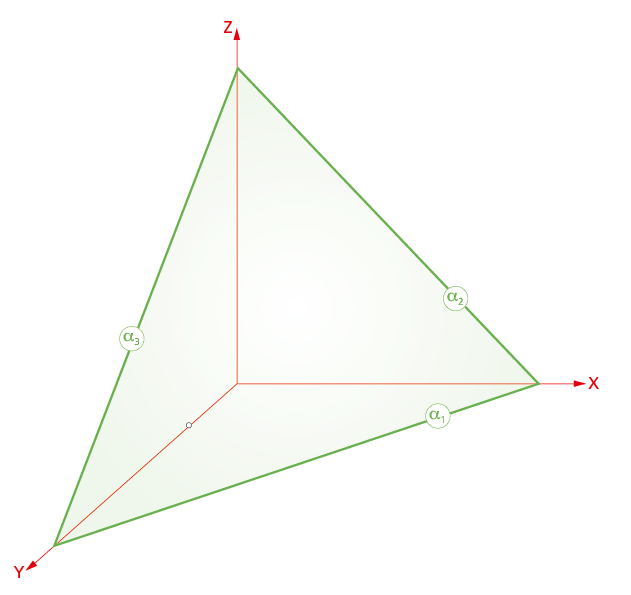
8.1.1 Planos que cortan a los ejes
Es el caso del plano α que se muestra en la figura superior o en el plano ω de la figura del apartado 8.2 de esta U.D. Obsérvese cómo las parejas de trazas de los planos representados concurren en puntos de los ejes. En el plano ω, las trazas ω1 y ω3 se cortan en un mismo punto del ejeaY en su parte negativa (por detrás del plano coordenado XZ) .
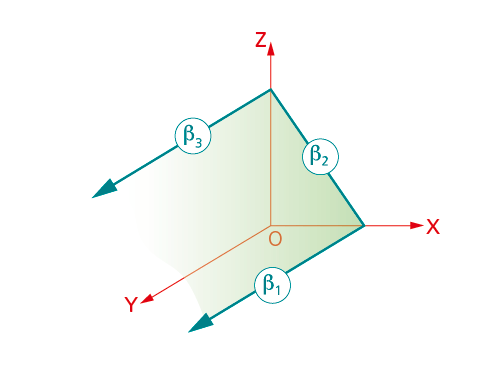
8.1.2 Planos proyectantes
Planos perpendiculares a los coordenados. En la figura de la derecha se representa un plano b proyectante vertical (perpendicular al cuadro).
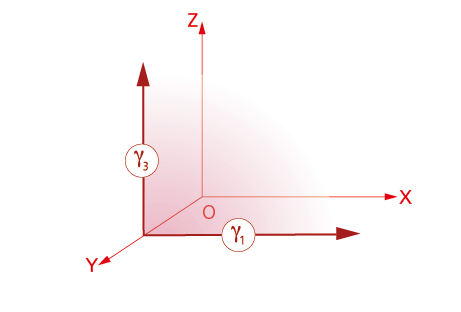
8.1.3 Planos paralelos a los coordenados.
En la figura se ha representado un plano γ paralelo al coordenado XZ.
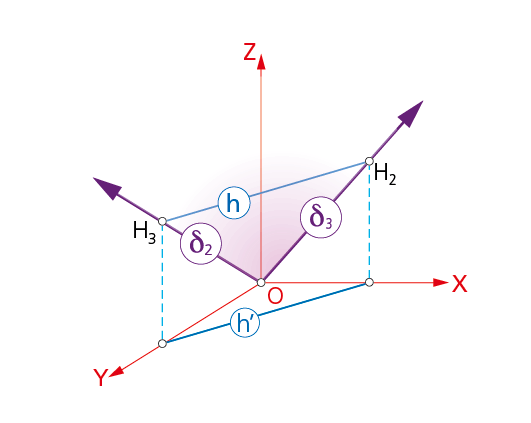
8.1.4. Planos que pasan por el origen.
En la figura, el plano d que pasa por el origen O, punto en el que concurren las trazas S2 y S3 del plano.
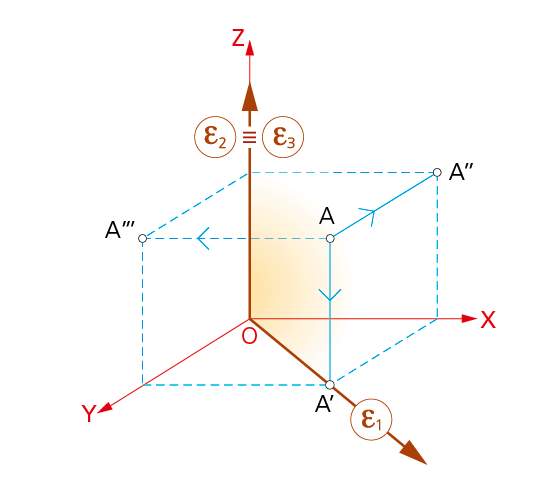
8.1.5. Planos que contienen a un eje.
En la figura, el plano e que contiene o pasa por el eje vertical Z.
8.2 Pertenencia a un plano.
Recuérdese que toda recta pertenece a un plano si tiene sus puntos traza sobre las trazas homónimas del plano que la contiene.
Análogamente, para que un punto pertenezca a un plano es preciso que dicho punto se encuentre sobre una recta contenida en dicho plano.
• Recta horizontal del plano.
La recta h, contenida en un plano cualquiera ω, es paralela al plano horizontal. Las proyecciones h (directa) y h’ (proyección horizontal) serán paralelas a la traza ω1 y las otras dos proyecciones h” y h’” serán paralelas a los ejes X e Y respectivamente.
• Recta frontal del plano.
Recta, tal como la f paralela al plano frontal XZ. Las proyecciones f (directa) y f” (proyección vertical) son paralelas a la traza ω2; f’ lo será al eje X y f’’’ al eje Z. Obviamente, no posee traza frontal (F2), dado que es paralela al plano del cuadro (XZ).
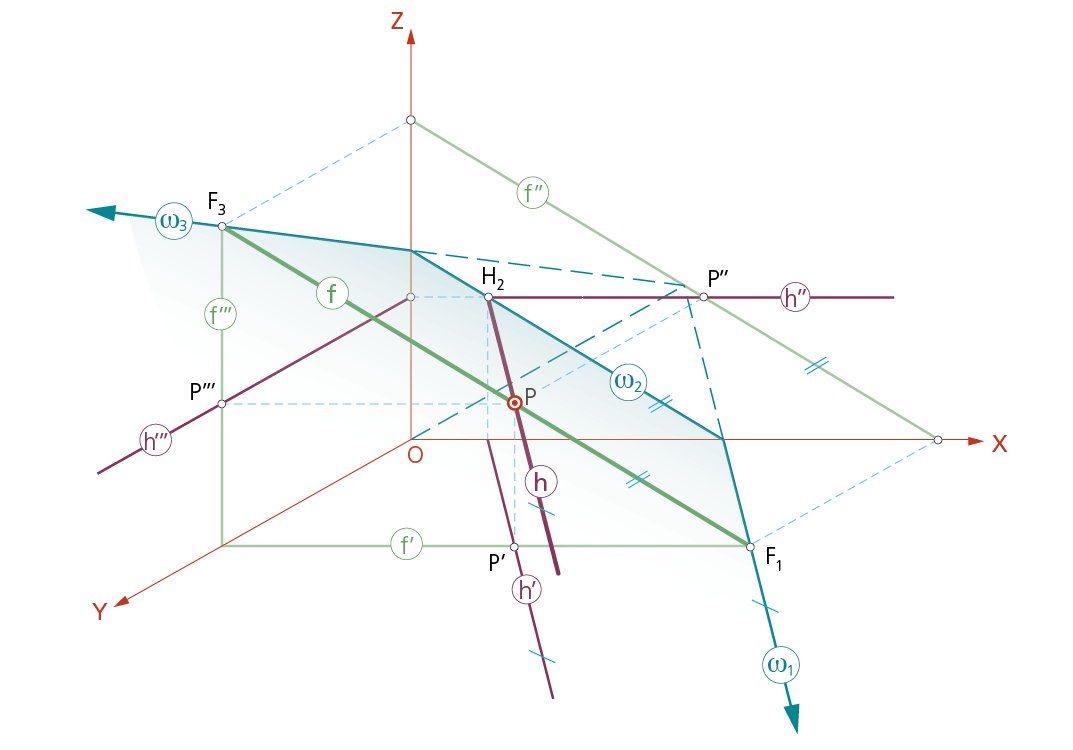
Recta horizontal (h) y frontal (f) del plano w que pasan por un punto P.