FORMAS POLIGONALES
PLUS
Unidad 3
LA COMPOSICIÓN MODULAR
La subdivisión de un triángulo equilátero o un cuadrado en partes iguales, mediante el trazado de rectas equidistantes entre sí y paralelas a sus lados, nos ofrece el ejemplo más simple y elemental de estructura o red modular, esto es, de estructura o malla formada por submódulos de la figura de partida: el triángulo equilátero y el cuadrado.
Todo submúltiplo así obtenido es un módulo, término que en la acepción moderna sirve para indicar una forma (elemento base) o conjunto unitario de piezas que se repiten en una construcción de cualquier tipo, haciéndola más fácil, regular y cómoda.
La red de líneas que subdividen regularmente la superficie modular toma el nombre de parrilla o retícula de referencia, siendo por tanto ambos conceptos términos sinónimos.
Además de la estructura de retícula cuadrada, es de gran interés la estructura modular del triángulo equilátero. Su malla sugiere inmediatamente la posibilidad de determinar varios módulos de forma distinta de la del módulo base (el triángulo equilátero) del que derivan, tales como el rombo, el trapecio isósceles y el hexágono regular, respectivamente compuestos por la adición de dos, tres o seis módulos base.
Las posibilidades creativas son enormes, tanto en la red modular de triángulos equiláteros como en la red modular de cuadrados. Tan solo debes dejar libre tu mente e ir investigando con la agrupación de formas modulares como las descritas en las ilustraciones, a modo de teselas. Las formas modulares obtenidas pueden decorarse de diferentes maneras, consiguiendo de este modo sensaciones plásticas diferentes, incluso cambian do únicamente los colores. También puedes obtener efectos utilizando solamente colores neutros (el blanco, el negro y toda la gama de grises).
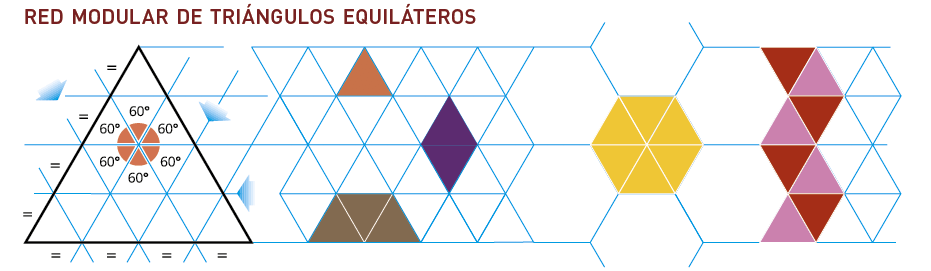
Módulos obtenidos con la estructura triangular: hexágonos, rombos y trapecios isósceles.
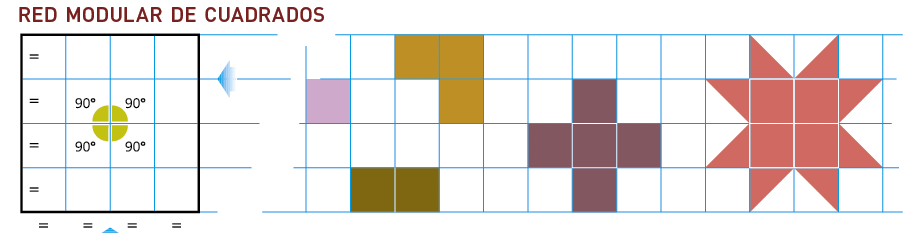
Generación de la red modular de cuadrados.
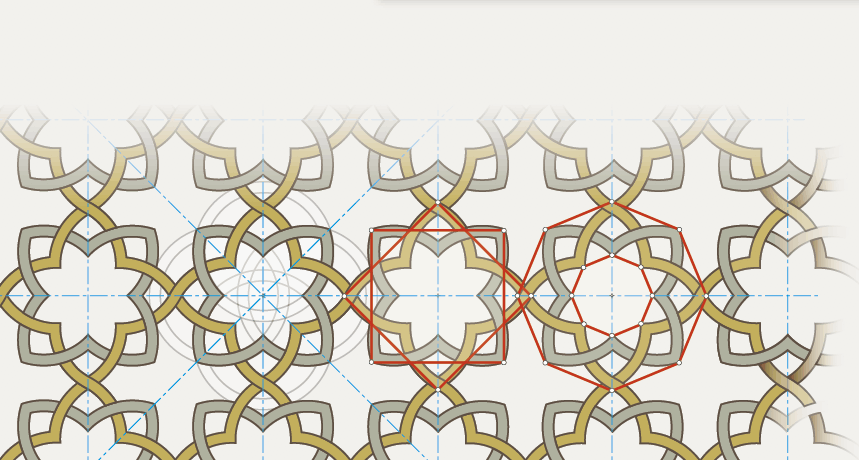
Los árabes fueron grandes maestros del arte del ornamento geométrico. En la Alhambra de Granada, construida entre los siglos XIII-XV, muchos de los pavimentos y mosaicos de suelos y paredes están decorados con baldosas de cerámica vidriada de colores cálidos, siguiendo esquemas compositivos de grupos de simetría, como el mostrado en este ejemplo a partir de polígonos.
La habilidad y virtuosismo de que gozaban los árabes en este período de la historia refleja la supremacía en el conocimiento de la geometría y su asidua aplicación al dibujo geométrico abstracto, determinada por la prohibición religiosa de representar la figura humana.

La calzada de los gigantes.
Hace unos 60 millones de años, el progresivo enfriamiento de una caldera volcánica fracturó poco a poco la lava de su colada pero, a l a vez, evitó su desplazamiento por el terreno (proceso geológico conocido como diaclasa) originando la formación de unas 40000 columnas de basalto de forma hexagonal que hoy recorren parte de la costa del condado de Antrim, en el norte de Irlanda.
POLÍGONOS EN LA NATURALEZA
Aunque parezca mentira, las formas geométricas son relativamente sencillas de encontrar en nuestro entorno de forma natural. Es cierto que no serán tan precisas como una forma geométrica realizada con los útiles de dibujo sobre el papel, pero a veces la naturaleza puede resultar sorprendente y precisa en la formación de elementos poligonales. A continuación te mostramos algunos ejemplos encontrados de forma natural a nuestro alrededor.