FORMAS POLIGONALES

5• POLÍGONOS ESTRELLADOS

Partiendo de un polígono regular, y cambiando el orden de la unión de sus vértices –es decir, uniendo sus vértices de forma no consecutiva– se construyen otros polígonos diferentes llamados estrellados o cóncavos, cuyos lados y ángulos son iguales.

Estas figuras geométricas de gran belleza son muy utilizadas en las arquitecturas propias del arte clásico español y en particular en las arquitecturas y edificaciones del arte árabe.

El polígono estrellado se cierra en el mismo vértice que se comenzó: su trazado puede hacerse sin levantar el lápiz del papel. El número de vueltas necesarias para cerrar el polígono se denomina «pasos». 

Así, por ejemplo, un polígono estrellado pentagonal (cóncavo) se obtiene de un pentágono convexo uniendo alternativamente sus vértices, lo que trae consigo haber dado dos vueltas completas y, por tanto, haber obtenido un polígono de «paso 2».
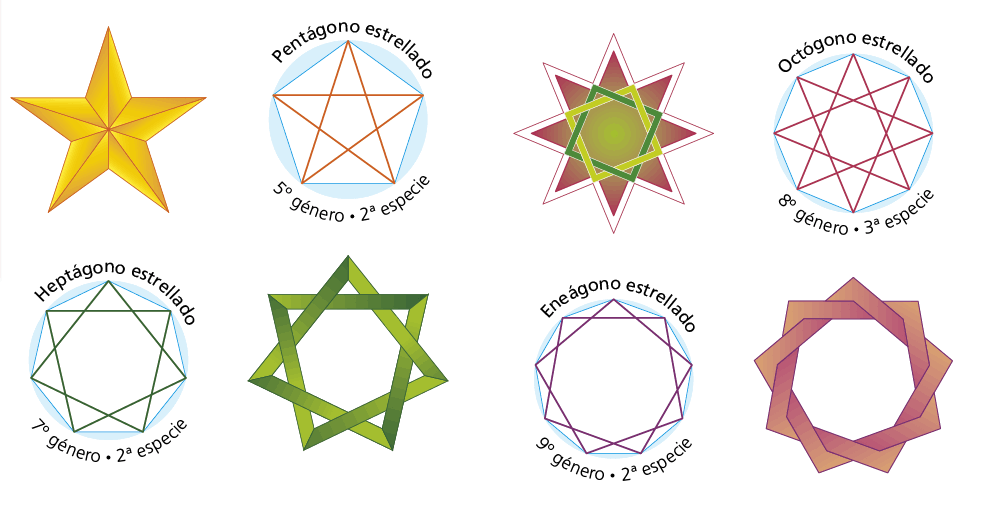
En los polígonos estrellados existen dos términos importantes que identifican a cada uno de ellos:
• El género: número de cuerdas empleadas para el trazado del polígono (igual al número de puntas o vértices).
• La especie: número de vueltas que hay que dar a la circunferencia para cerrar el polígono (igual al número de «pasos»).