SISTEMA DIÉDRICO
Síntesis del Sistema diédrico
Unidad 6
1- SÍNTESIS DEL SISTEMA DIÉDRICO
Como se ha indicado en la Unidad Didáctica anterior, el sistema diédrico es el sistema de representación más importante y base para el estudio y análisis de los demás. Aporta una información más detallada y analítica del objeto que ningún otro sistema de representación, pues cada detalle es resuelto por un dibujo a escala verdadera (sin deformación lineal ni angular) más la información de sus medidas escritas en cifras de lectura directa.
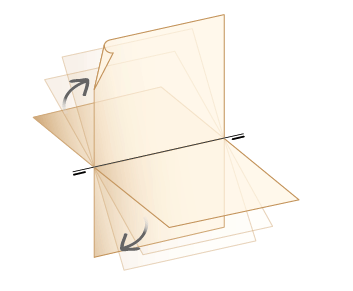
1.1 Planos de proyección.
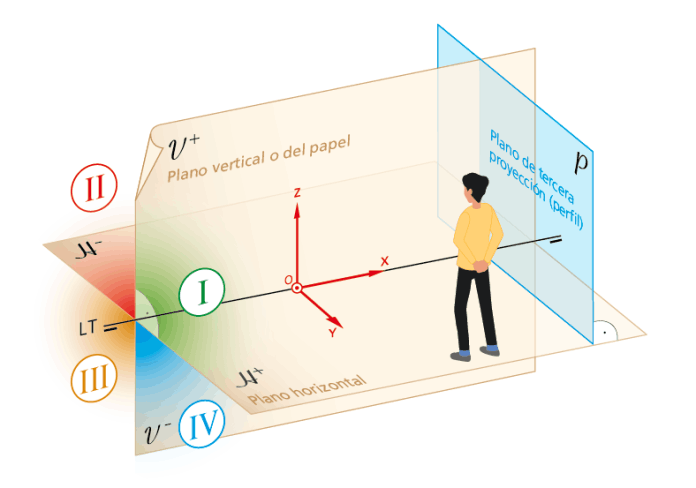
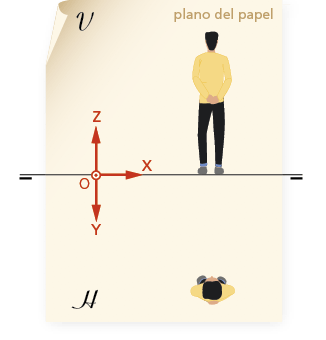
En este sistema se utiliza la proyección ortogonal y sus elementos principales son los llamados planos de proyección, o planos de referencia fundamentales: el Plano Horizontal (H), que se supone en posición horizontal, y el Plano Vertical (V), que es perpendicular al H.
Para pasar de las tres dimensiones del espacio a las dos dimensiones del plano, hacemos coincidir el plano horizontal con el plano vertical –utilizado como plano del dibujo–, y todo lo que está situado sobre el horizontal H se superpone sobre el vertical haciéndole girar, alrededor de la recta intersección de ambos (LT).
PLANOS DE PROYECCIÓN
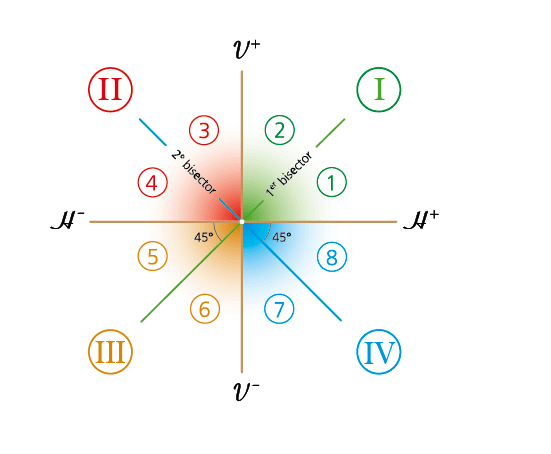
Ambos planos de referencia V y H se cortan bajo un diedro recto y dividen al espacio en cuatro regiones denominadas cuadrantes:
- Primer cuadrante (I): espacio comprendido entre el semiplano horizontal anterior (H+) y el semiplano vertical superior (V+).
- Segundo cuadrante (II): espacio comprendido entre el semiplano horizontal posterior (H-) y el semiplano vertical superior (V+).
- Tercer cuadrante (III): espacio delimitado por el semiplano horizontal posterior (H-) y el semiplano vertical inferior (V-).
- Cuarto cuadrante (IV): espacio delimitado por el semiplano horizontal (H+) y el vertical (V-).
Los puntos se designan por letras mayúsculas del alfabeto latino. Así, por ejemplo, un punto A viene dado por sus proyecciones ortogonales A’, A’’y A’’’ sobre el plano horizontal (H), el plano vertical (V) y el plano perfil (P) respectivamente. Asimismo, las rectas se designan por letras minúsculas del alfabeto latino. Así, una recta r del espacio viene dada por sus proyecciones r’, r’’ y r’’’ sobre los planos de proyección H, V y P respectivamente.
En el plano del papel las proyecciones muestran la planta y el alzado de la figura representada.
1.2 Línea de tierra (LT).
Es la recta común a los planos de proyección. Se trata de la recta virtual alrededor de la cual imaginamos gira el plano horizontal (H) para superponerse sobre el vertical (V). Su notación simplificada es LT, y se representa en línea fina con dos trazos gruesos y cortos en sus extremos o bien por una línea fina de trazos y doble punto; es lo que genéricamente puede entenderse como línea de plegamiento del plano de proyección horizontal (H) sobre el plano de proyección vertical (V) o plano del papel
1.3 Plano de la tercera proyección.
Es aquel perpendicular a los dos principales de proyección. Se trata, por tanto, de un plano de perfil o plano lateral, de ahí su designación mediante la letra P. Se usa para facilitar las representaciones y mejorar la comprensión de lo que se proyecta sobre los planos de referencia.
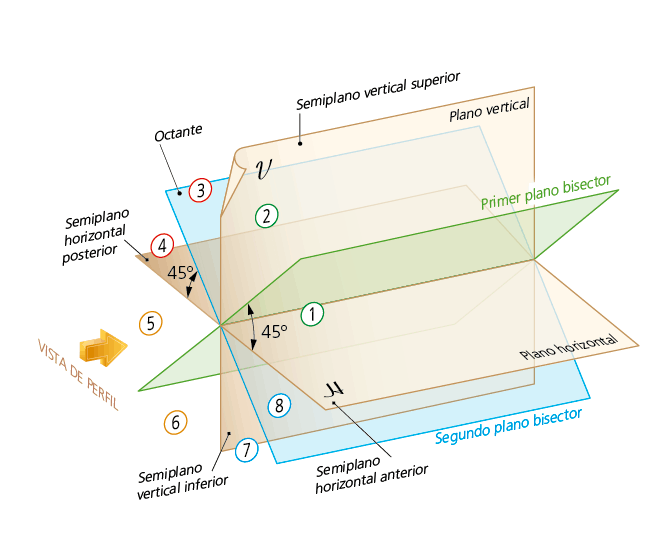
1.4 Planos bisectores.
Son dos planos (primer y segundo bisector) perpendiculares entre sí, que dividen a cada diedro de 90º en dos partes iguales, resultando el espacio dividido en ocho octantes o diedros de 45°. Todos los puntos contenidos en estos planos equidistan de los planos de proyección horizontal H y vertical V y, por tanto tendrán, en valor absoluto, igual cota que alejamiento.
1.5 Sistema de coordenadas.
Antes de intentar la solución gráfica de un ejercicio, es necesario describir la posición relativas de los datos. Uno de los sistemas más utilizados es el de los ejes o coordenadas cartesianas X, Y, Z; donde la localización de cualquier punto puede llevarse a cabo si se describe su posición con respecto a dichos ejes.
El origen se sitúa en un punto de la LT, el eje X –coordenada desplazamiento– se extiende con su parte positiva hacia la derecha, el eje Y –coordenada alejamiento–, perpendicularmente al anterior y con su parte positiva hacia el observador y, el eje Z –coordenada altura o cota–, perpendicular a los anteriores y con sentido positivo hacia arriba.