SISTEMA DIÉDRICO
Contenido complementario
Unidad 6
Rectas singulares para definir un plano:
RECTA DE MÁXIMA PENDIENTE, DE MÁXIMA INCLINACIÓN Y DE PERFIL
Se entiende por «pendiente de una recta» a la razón o cociente entre la diferencia de cotas de dos puntos de la misma y la distancia entre sus proyecciones horizontales. Asimismo, se llama «inclinación de una recta» al cociente entre la diferencia de alejamientos de dos cualesquiera de sus puntos y la distancia entre sus proyecciones verticales. Ambos conceptos son idénticos: el de pendiente referido al plano horizontal y el de inclinación referido al plano vertical.
Las rectas –contenidas en un plano– con pendiente máxima se caracterizan por ser perpendiculares a la traza horizontal del plano que las contiene, lo que trae consigo que su correspondiente proyección horizontal sea perpendicular a la traza horizontal de dicho plano.
Así, la recta m, de máxima pendiente del plano β tiene su proyección horizontal m’ perpendicular a la traza horizontal β1. Dicho de otra forma: la recta m y su proyección m’ se encuentran y definen un plano que es perpendicular al plano β.
Análogamente, las rectas de máxima inclinación de un plano tienen su proyección vertical perpendicular a la traza vertical de dicho plano. Es como girar la hoja de papel 180° e imaginar las trazas del plano cambiadas: la recta de máxima pendiente descrita anteriormente se convierte en recta de máxima inclinación.
La singularidad de estas rectas nos muestra que no sólo es posible definir un plano de cualquiera de las cuatro maneras descritas en esta UD, sino que también es posible su determinación teniendo como único dato una recta de máxima pendiente o una recta de máxima inclinación de dicho plano. En efecto, dada la recta m por sus proyecciones diédricas m’-m’’, para determinar las trazas β1-β2 del plano definido por la recta, se procede como sigue:
- Se hallan los puntos traza horizontal M1 (M’1- M’’1) y vertical M2 (M’2 -M’’2 ) de la recta, y por M’1 se dibuja la perpendicular a la proyección m’, que resultará ser la traza horizontal β1 del plano definido por la recta m
.
-Dicha traza corta a la LT en un punto que, unido con M’’2 , determina la traza vertical β2 .
Análogo proceso se llevaría a cabo en el caso de tener que determinar las trazas de un plano dado por una recta de máxima inclinación del mismo; es el caso de la recta i.
En la segunda ilustración se presenta la presentación espacial y diédrica de una recta de perfil de un plano. Es aquella recta contenida en el plano y perteneciente a un plano de perfil, siendo perpendicular a la LT. Dicho de otra forma: una recta de perfil p es la intersección del plano γ, a que pertenece, con el plano de perfil que la contiene.
Sus proyecciones son perpendiculares a la LT y, como toda recta de perfil, se define conociendo dos de sus puntos. En la figura la recta p pasa por el punto A y sus puntos traza horizontal P1 y vertical P2 se encuentran en las trazas horizontal γ1 y vertical γ2, respectivamente, del plano que la contiene.
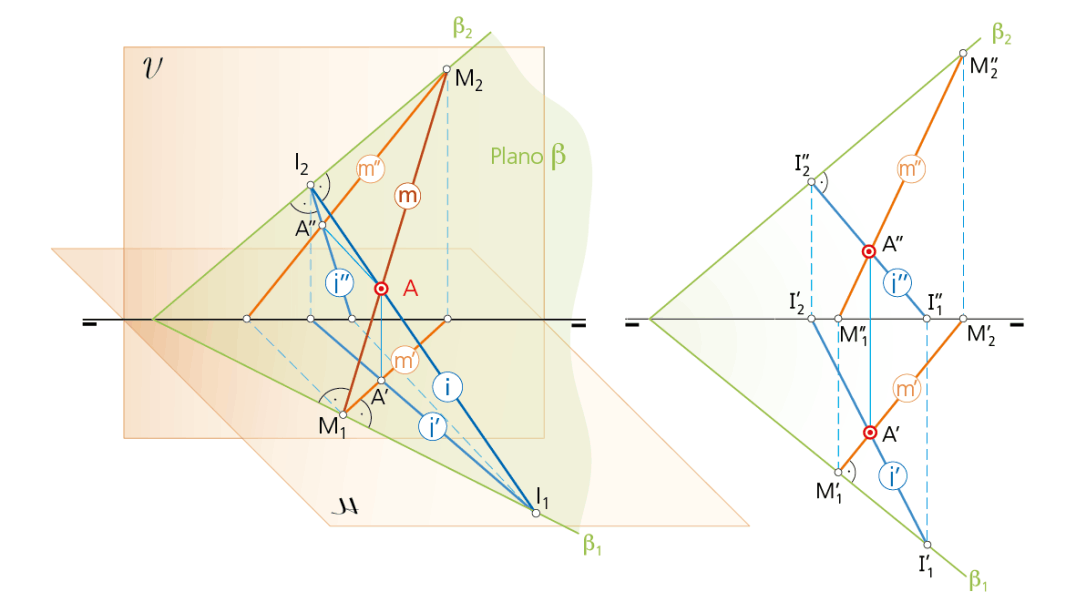
Recta de máxima inclinación y recta de máxima pendiente.
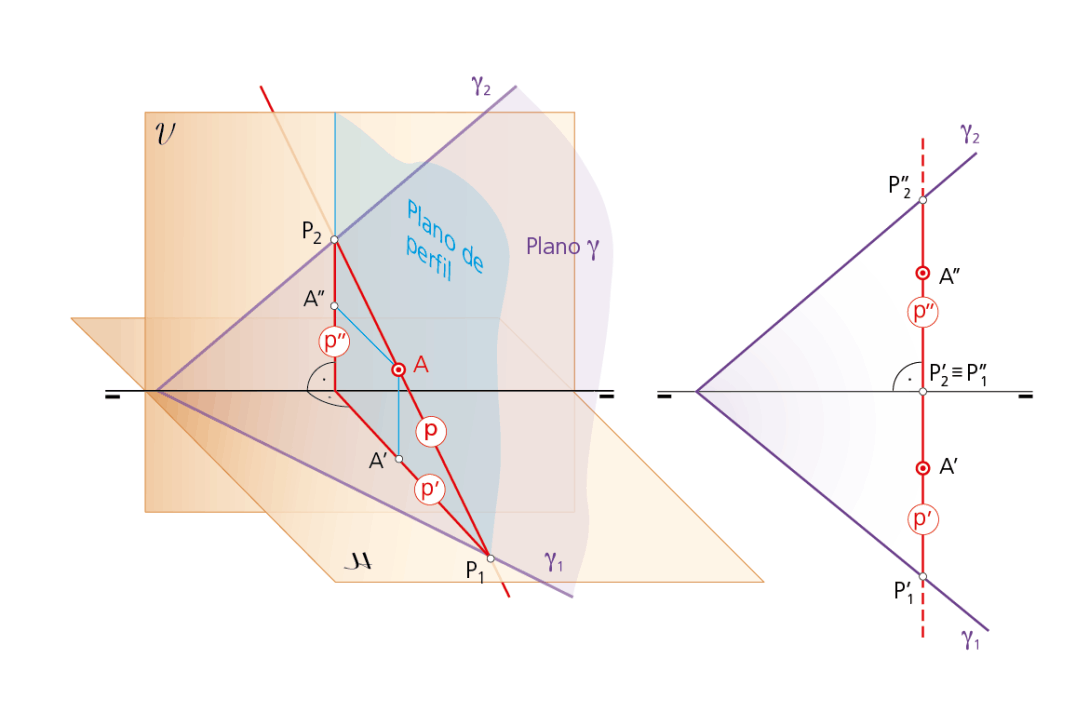
Recta de perfil de un plano.