5 - EL PLANO
SISTEMA DIÉDRICO
Síntesis del Sistema diédrico
Unidad 6
Geométricamente un plano puede venir determinado por:
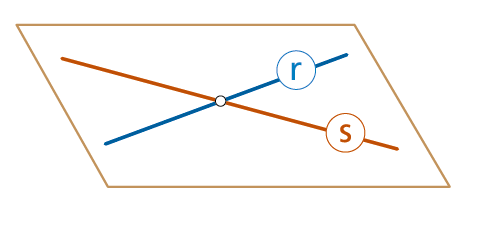
Dos rectas r y s que se cortan.
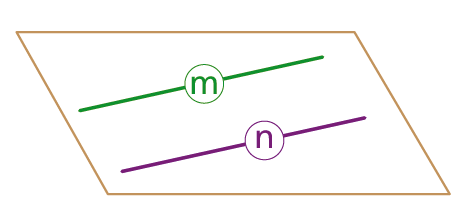
Dos rectas m y n paralelas.
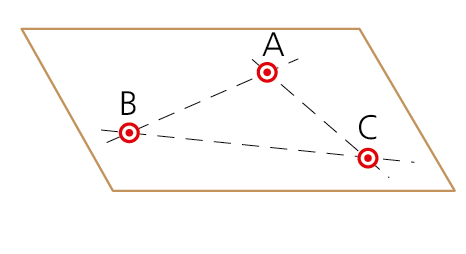
Tres puntos A, B y C no alineados.
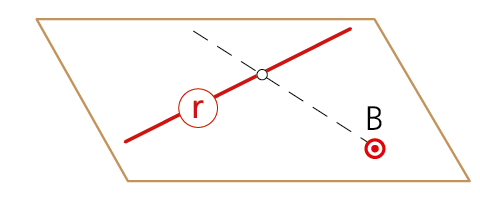
Una recta r y un punto B exterior.
5.1 Representación del plano por coordenadas.
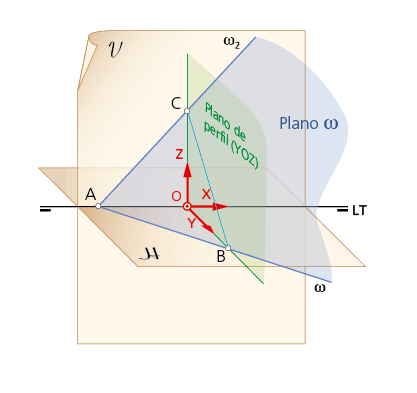
Al igual que sucede en la ubicación de un punto del espacio, en la determinación de un plano ω (ver figura inferior) intervienen las tres coordenadas cartesianas que posicionan todo plano con respecto a los planos principales de proyección.
Así, un plano viene expresado, analíticamente, de la forma ω (x,y,z), siendo:
• X: la distancia del origen O al punto A donde concurren las trazas del plano.
• Y: alejamiento de la traza horizontal ω1 respecto del origen
• Z: cota de la traza vertical ω2 respecto del origen.
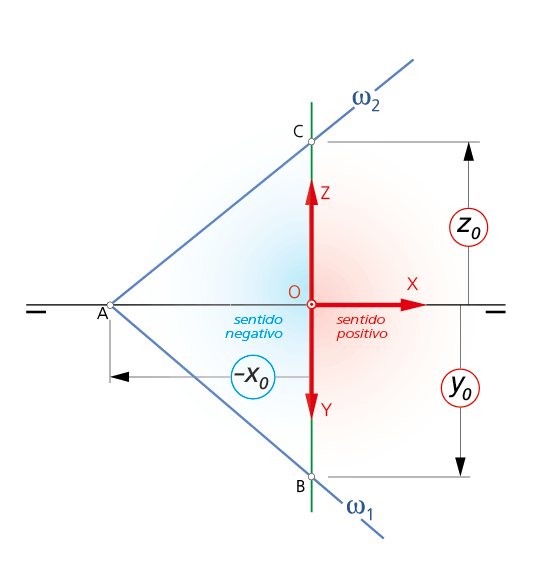
Representación diédrica de un plano dado por sus coordenadas cartesianas: ω(-x0, y0, z0).
5.2 Representación del plano por sus trazas.
Tradicionalmente, la representación de un plano se lleva a cabo mediante sus trazas, es decir, dibujando las rectas de intersección del plano con los de proyección. La traza horizontal del plano α, designada como α1, es la intersección con el plano horizontal H; y la traza vertical, designada como α2, es la intersección con el plano vertical V. Si estas dos trazas de un plano se cortan en un punto de la LT dicho punto se denomina vértice del plano.
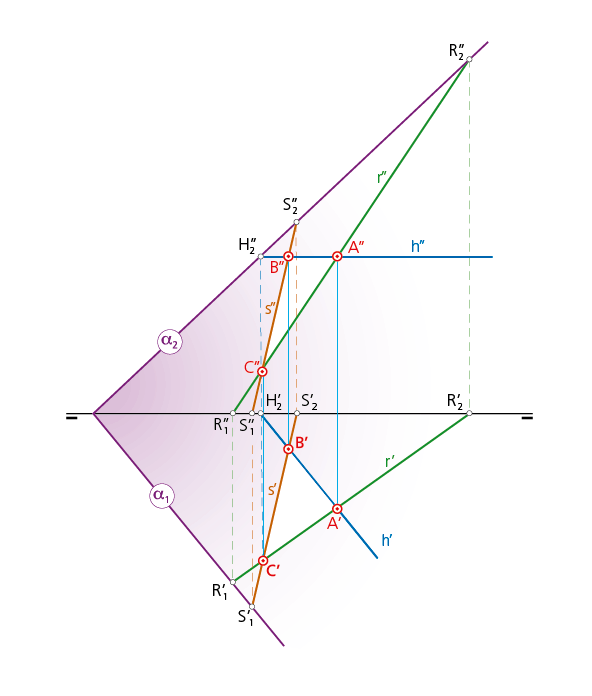
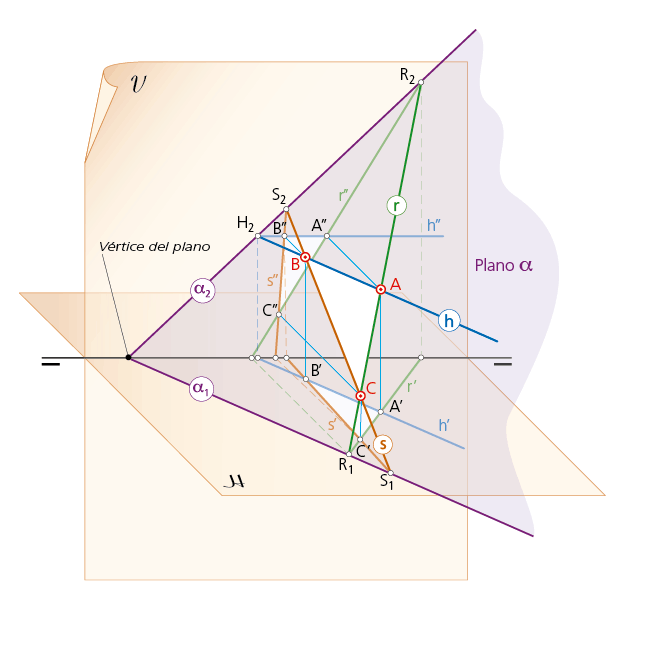
En la figura el plano α se determina por tres puntos A, B, C; por dos rectas que se cortan (r y h, s y h o bien por r y s) o por una recta (cualquiera de las anteriores) y un punto exterior a ella. En cualquier caso, las rectas que lo constituyen tienen sus puntos traza en las trazas correspondientes del plano; así, el punto traza vertical H2 de la recta horizontal h, se encuentra en la traza vertical α2 del plano que contiene a dicha recta. Lo mismo sucede con la recta s o la recta r. En definitiva, para dibujar cada traza de un plano (que son el lugar geométrico de los puntos traza de las rectas contenidas en él) se han de definir, previamente, al menos dos puntos traza de dos rectas de dicho plano.
Perspectiva del plano y representación diédrica por sus trazas
5.3 Pertenencia de punto o recta a un plano.
Para que una recta pertenezca a un plano los puntos traza de la recta deben estar sobre las trazas homónimas del plano que la contiene. Así, en la figura la recta r, cuya traza horizontal es R1, se encuentra en la traza horizontal α1 del plano; al igual que la traza vertical R2 se encuentra sobre la traza vertical α2 del plano que contiene a dicha recta. Para verificar la pertenencia de un punto a un plano se hace pasar por él una recta cualquiera perteneciente al mismo (de las infinitas posibles); es decir, que cumpla las condiciones anteriores. Por su sencillez es aconsejable utilizar horizontales o frontales del plano. Así, el punto A pertenece al plano α por estar contenido en una recta, tal como la h o la recta r, perteneciente al mismo.