ELEMENTOS GEOMÉTRICOS

5- RECTAS ANTIPARALELAS

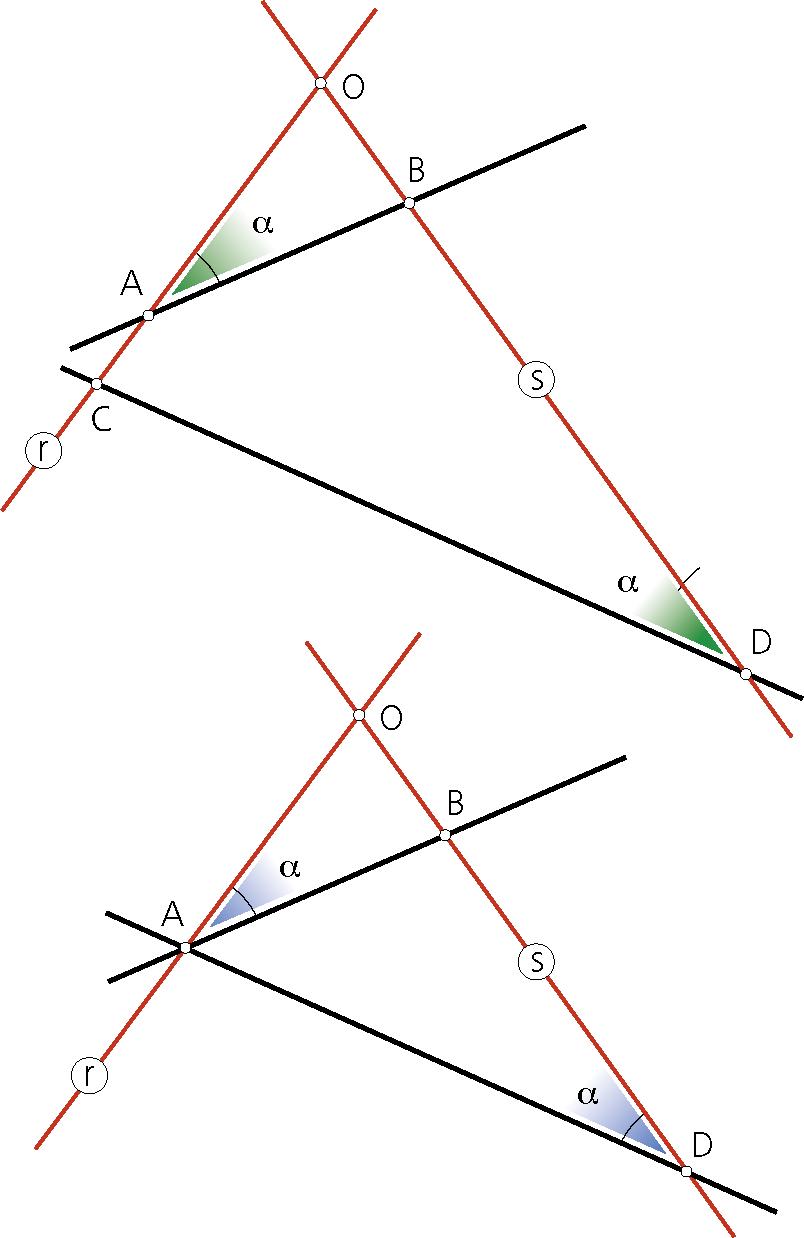
«Dos rectas AB y CD se dice son antiparalelas respecto de otras dos r y s cuando el ángulo a que forma la recta AB con la recta r es igual al ángulo que forman la recta CD con la recta s».
Los triángulos OAB y OCD (figura al pie-superior) son semejantes por tener los tres ángulos iguales y, por tanto, se verifica:
OA/OD=AB/CD=OB/OC.

Cuando las rectas antiparalelas pasan por un mismo punto A de una de ellas (figura al pie-inferior),Se verifica:
OA2=OB·OD
Obsérvese que los triángulos OAB y OAD son semejantes por tener los tres ángulos iguales y por ello: OA/OB=OD/OA, con lo que queda demostrado la relación anterior.

Resultando por tanto que:
• «El producto de las distancias desde el vértice de un ángulo, a los puntos de corte de cada lado de dicho ángulo con dos rectas antiparalelas es constante (OA2=OB·OD)».
• «Si dos rectas antiparalelas se cortan sobre un punto de los lados de un ángulo, la distancia del vértice a este punto es media proporcional entre las distancias del vértice a los puntos en que el segundo lado corta a dichas rectas». En ambos casos se verifica el recíproco.