SISTEMA DIÉDRICO II
Síntesis del Sistema diédrico
Unidad 7
1• INTERSECCIÓN DE PLANOS POR SUS TRAZAS
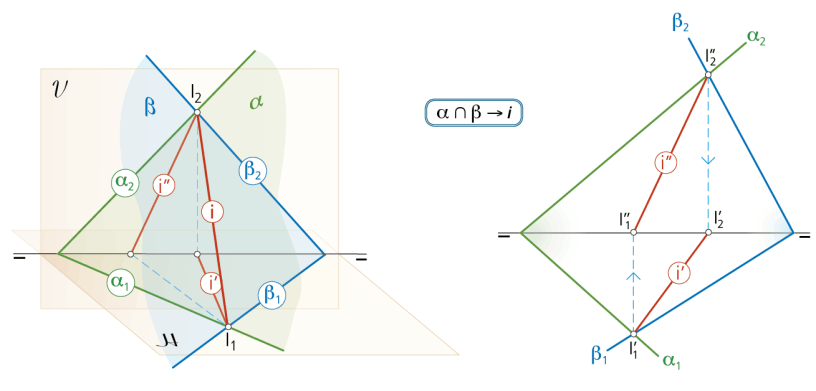
1.1 Intersección de dos planos conocidas sus trazas: procedimiento general.
Dos superficies planas, no paralelas, se cortan según una recta.
Dicha recta intersección i al pertenecer a ambos planos α y β, verifica con cada uno de ellos las condiciones de pertenencia a un plano: su punto traza horizontal I1 estará en la intersección de las trazas horizontales α1 y β1 de los planos y, su punto traza vertical I2 en la intersección de las trazas verticales α2 y β2.
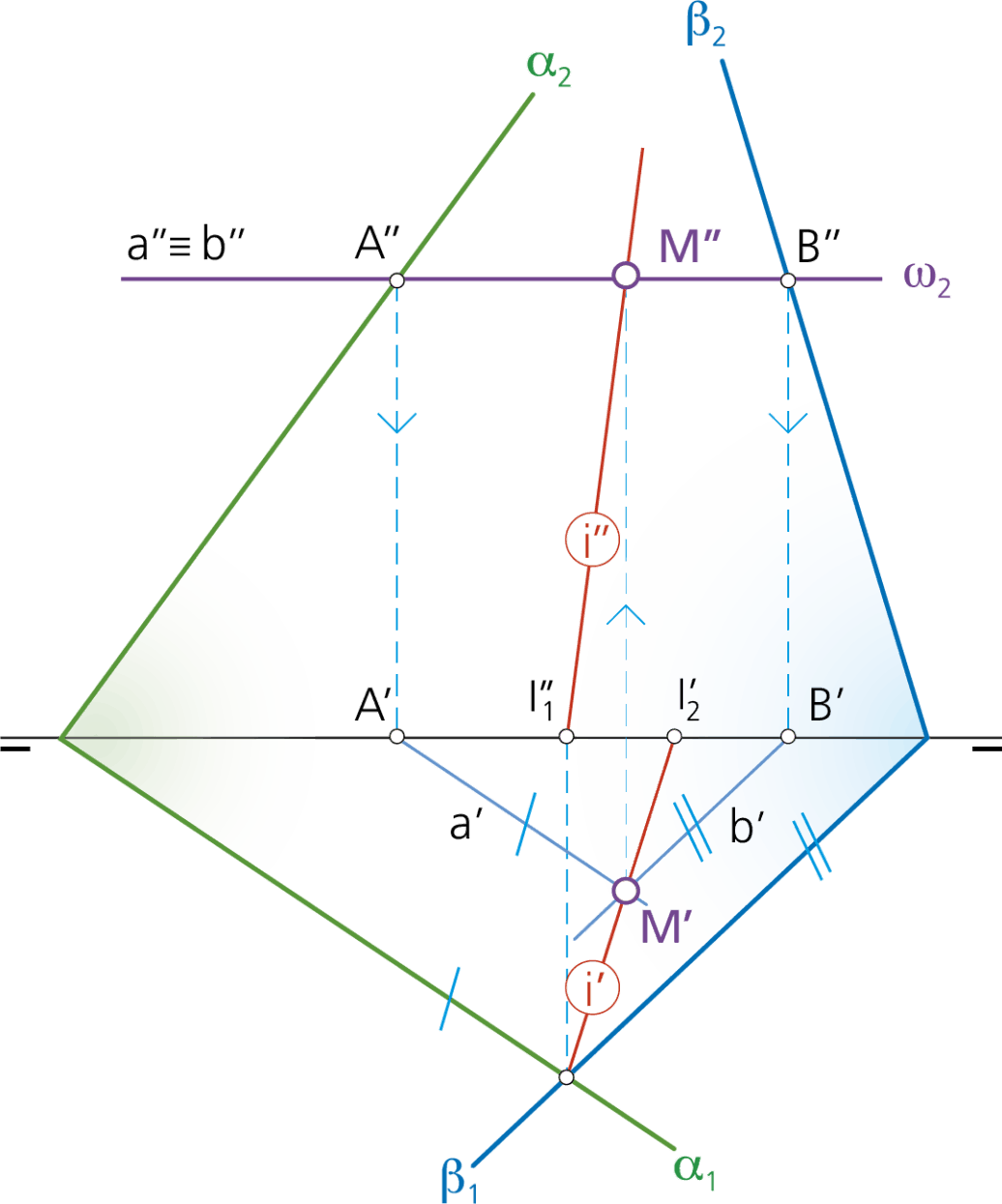
1.2 Intersección cuando las trazas de los planos se cortan fuera de los límites del dibujo.
Si las trazas de los planos se cortan fuera de los límites del papel, se emplea otro procedimiento alternativo para localizar la recta intersección de ambos planos: consiste en localizar puntos de la recta intersección diferentes de sus puntos traza. Para ello, se corta a los planos α y β dados, mediante planos auxiliares horizontales o frontales, del tipo ω o δ cómo muestra la ilustración al pie de estas lineas.
Por ello, se trazan paralelas a la LT para encontrar las trazas verticales A’’ y B’’ de las rectas a y b. Las proyecciones horizontales a’ y b’ serán respectivamente paralelas a las trazas horizontales α1 y β1 de los planos. De esta forma se localiza el punto M’, proyección horizontal del punto M, perteneciente a la recta intersección de ambos planos.
Para localizar otro punto de la recta intersección y con ello definirla, se puede operar con planos frontales (por ejemplo el plano δ) como muestra el gráfico en perspectiva al pie de estas líneas. Así se obtendría otro punto N que unido con M determinaría la recta intersección.
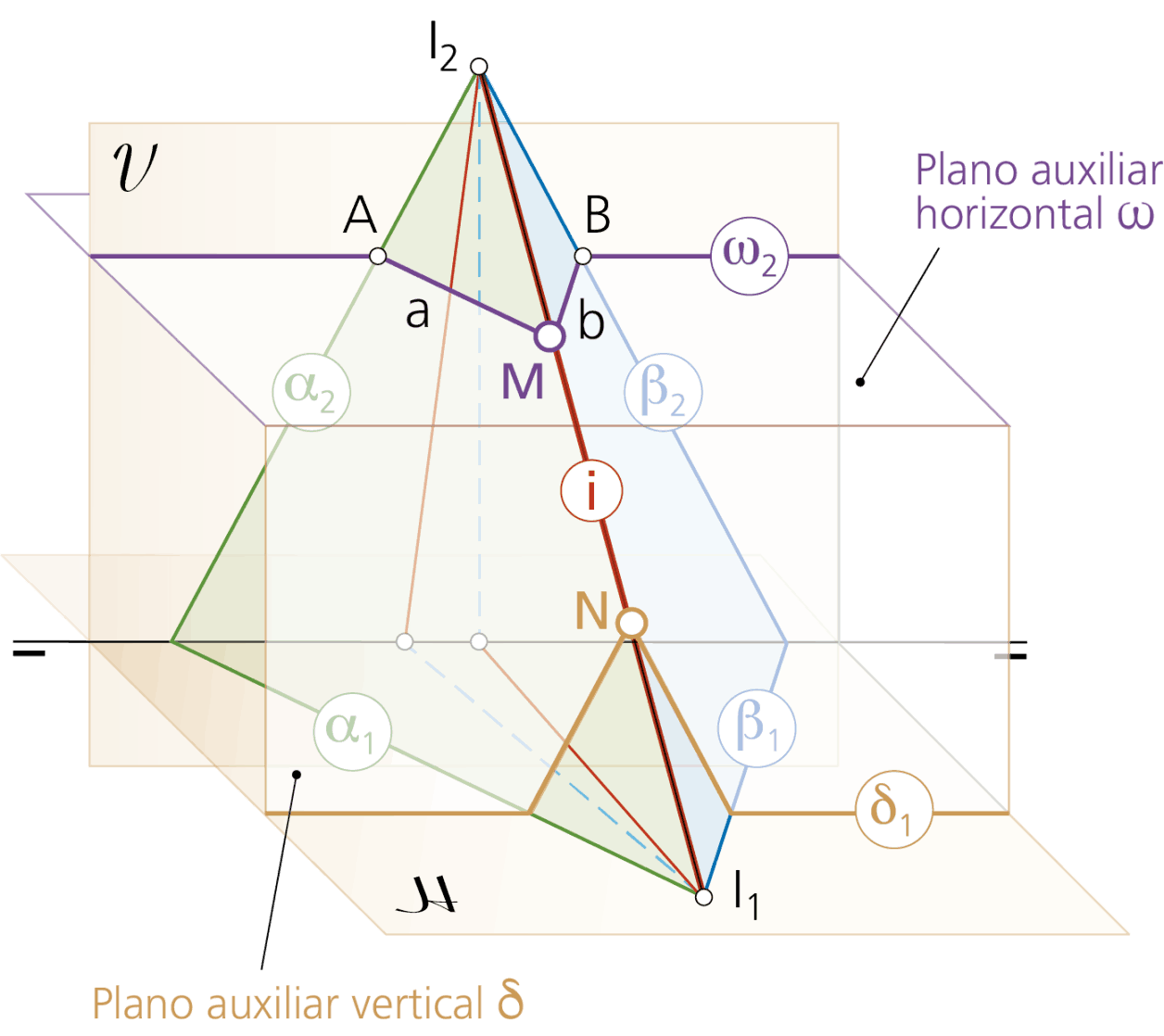
Gráfico en perspectiva para ayudar en la percepción espacial.
Muestra la recta intersección i de los planos α y β cuyas trazas verticales salen fuera de los límites de la superficie del dibujo. Por tan, se ha utilizado para determinar el punto M de la recta , un plano auxiliar horizontal que, unido al punto traza horizontal I1, define la recta intersección de los planos α y β considerados.trum massa.