SISTEMA DIÉDRICO II
Síntesis del Sistema diédrico
Unidad 7
5 DISTANCIAS
Como se recordó en geometría plana, hablar de distancia es hallar la verdadera magnitud del segmento que une dos elementos geométricos. Siempre, claro está, partiendo de su representación en el sistema diédrico.
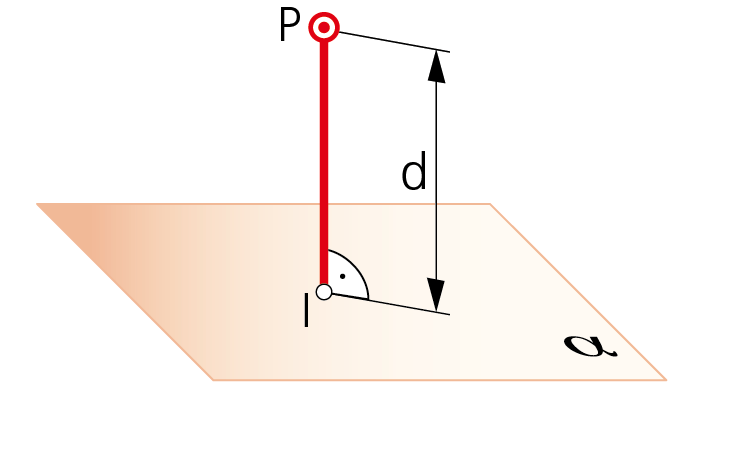
5.a. Distancia de un punto a un plano.
La distancia de un punto P a un plano α es la magnitud del segmento perpendicular al plano definido por el citado punto P y su punto intersección I con dicho plano. Esto es, la magnitud PI..
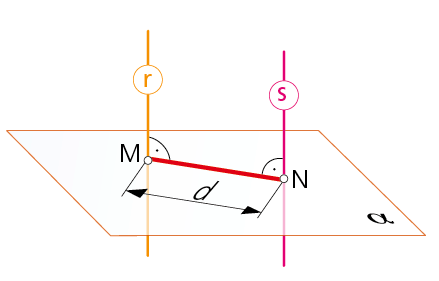
5.b. Distancia de un punto a una recta.
La distancia de un punto Q a una recta r, viene dada por la longitud existente entre dicho punto y el punto J de corte de la recta con la perpendicular a ella trazada desde dicho punto Q. Esta distancia se consigue trazando por Q un plano α perpendicular a la recta r dada y hallando el punto intersección J de la recta r con el plano α. La magnitud QJ es la solución buscada
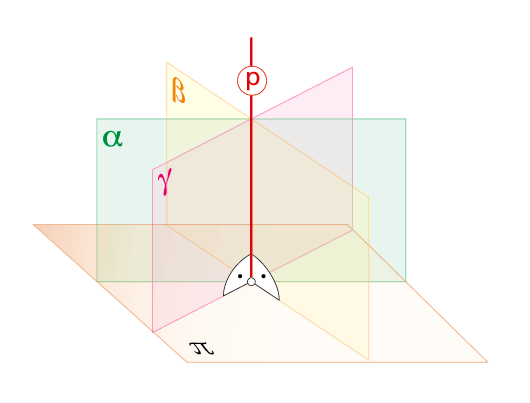
5.c. Distancia entre rectas paralelas.
«Un plano a, b... será perpendicular a otro π, cuando contenga a una recta p perpendicular al mismo».Recíprocamente, el plano π será perpendicular a otros (α, β, g, …) cuando lo sea a su recta intersección (p)». Todos los planos del haz que pasan por su recta común p son perpendiculares al plano π, y viceversa..
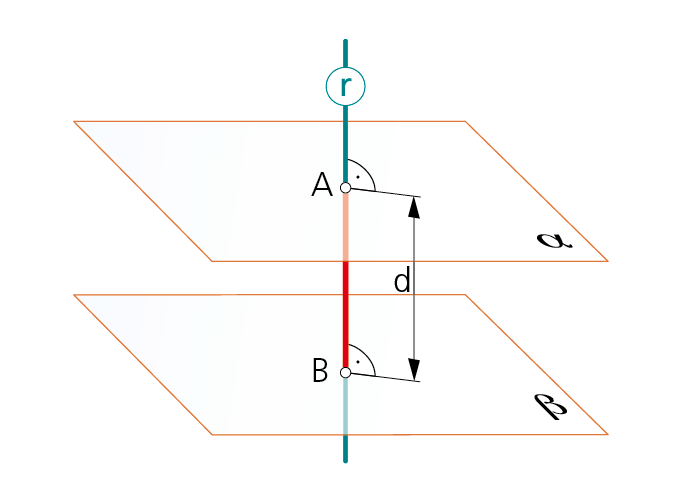
5.d. Distancia entre planos paralelos.
La distancia entre dos planos paralelos α y β queda determinada por la longitud del segmento AB, delimitado por los puntos de intersección, de cada uno de los planos considerados, con una recta r cualquiera que sea perpendicular a ambos planos.
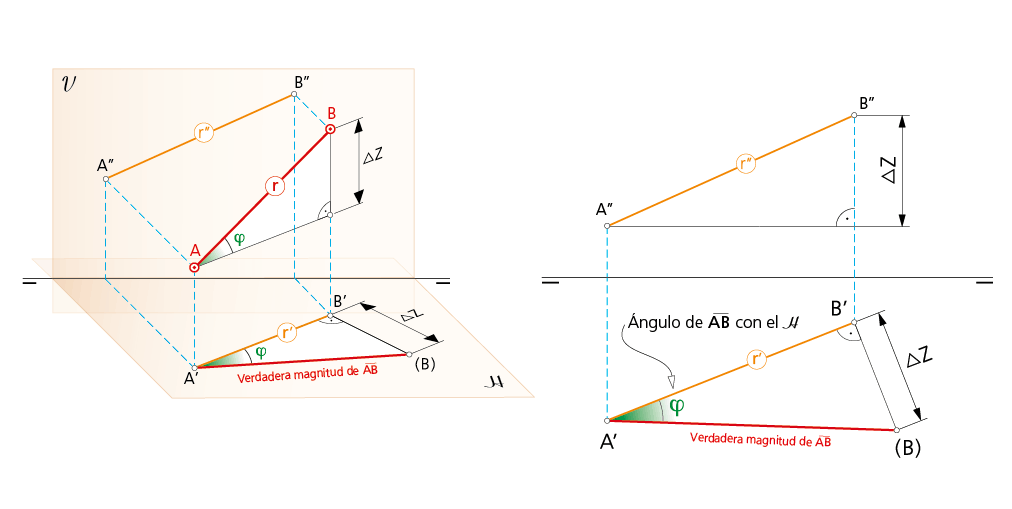
V.M. por diferencia de cotas o alejamiento en un segmento.
5.1.1. Verdadera magnitud de un segmento por diferencia de cotas o de alejamiento entre sus extremos.
En el gráfico a la derecha se representa una perspectiva de la posición de un segmento AB en el espacio y, a sus pies, las proyecciones diédricas del mismo.
Si se traza por A una paralela a la proyección horizontal A’B’, se obtiene, en el espacio, un triángulo rectángulo de catetos A’B’ y la diferencia de cotas entre ambos puntos (∆z), con hipotenusa el segmento AB.
Si se considera el segmento A’B’ proyección horizontal del segmento AB y por un extremo (en la figura el B’) se traza la perpendicular a A’B’, llevando la magnitud ∆z, se determina el punto (B) que, unido con A’, define la distancia real entre los puntos A y B (extremos del segmento considerado). El triángulo rectángulo A’B’(B), situado en el plano H, representa el abatimiento, sobre dicho plano, del triángulo espacial considerado en la ilustración que se acompaña.
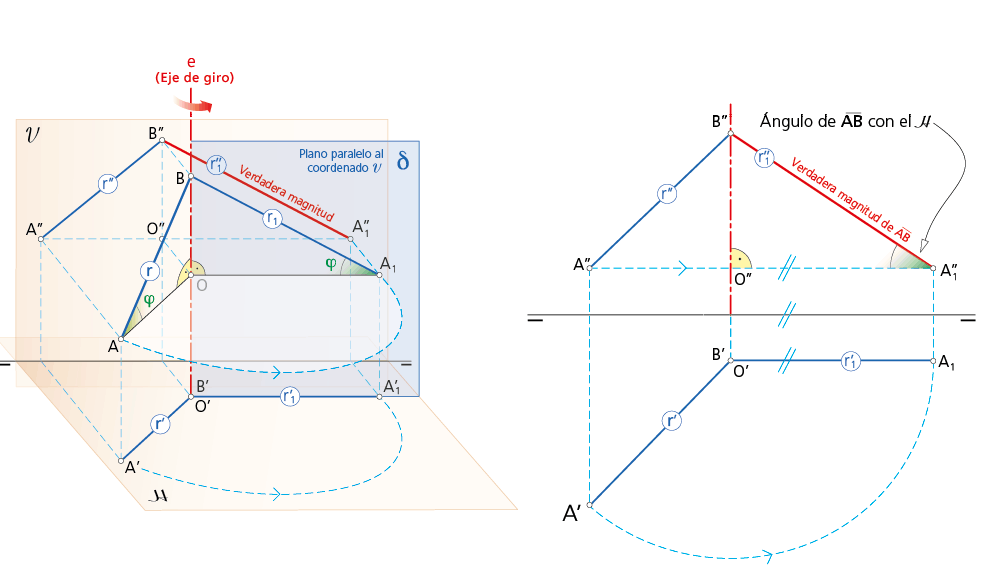
V.M. por giro de un segmento situándolo horizontal al plano vertical.
5.1.2. Verdadera magnitud de un segmento por giro del mismo, situándolo frontalmente.
Si giramos el triángulo rectángulo espacial, considerado anteriormente y contenido en un plano proyectante horizontal, alrededor del eje de giro BB’ (que contiene al punto B y es perpendicular al plano H sobre el que se proyecta el segmento AB) hasta que quede paralelo al plano vertical, el segmento AB, ahora A1B, queda situado frontalmente, es decir, paralelo al plano vertical de proyección V.
En esta situación, la proyección del segmento A1B sobre el plano vertical V, esto es, A’’1B’’, estará en verdadera magnitud, siendo A’’1B’’ = AB.