SISTEMA DIÉDRICO II
Contenido Complementario
Unidad 7
Intersección de recta y plano (DADO POR TRES PUNTOS O DOS RECTAS COPLANARIAS)
Cuando el plano no está dado por sus trazas sino por tres puntos A,B,C o por dos rectas AB y AC se usa el mismo procedimiento. En la fig. se ha considerado el plano proyectante horizontal que contiene a la recta r: su proyección horizontal r’ es coincidente con la proyección horizontal i’ de la recta i (recta intersección del plano proyectante π que contiene a la recta r con el plano ABC). Considerados los puntos 1’ y 2’ se obtienen sus correspondientes proyecciones verticales 1’’ y 2’’ que definen i’’ y con ello la proyección I’’ del punto intersección buscado. En los ejercicios de intersección de recta y plano se supone, en ocasiones, que el plano es opaco y se diferencian en la recta que lo atraviesa las regiones cuyas proyecciones son vistas u ocultas para un observador situado en el primer cuadrante.
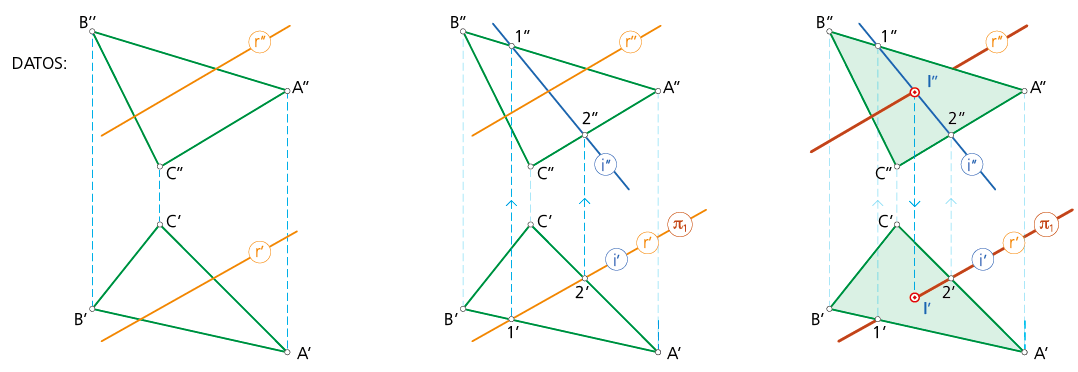
r ∩ ¬ABC → I
Método de la vista auxiliar (plano de canto)
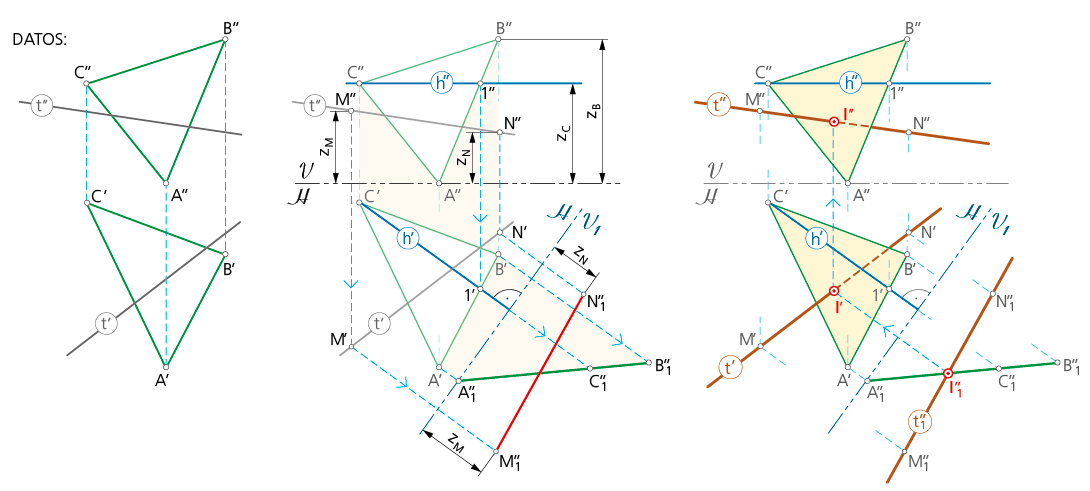
Este método también puede emplearse para encontrar la intersección entre una recta y un plano. En la fig. se dan como datos la recta t, definida por los puntos M y N, y el plano dado por tres puntos A,B y C . Para hallar el punto intersección de ambos elementos se procede como sigue:
Paso 1- En este método el plano ABC se debe visualizar como un plano de canto (proyectante vertical), lo que trae consigo determinar una vista auxiliar que le sitúe en esa posición; de tal manera que todos los puntos que están sobre él se encuentran representados sobre una recta de canto.
Con apoyo de una recta horizontal h (h’-h’’) del plano ABC se consigue la dirección de proyección hacia el nuevo plano vertical de referencia (V1) que transforma el plano oblicuo en proyectante vertical.
La nueva proyección de la recta t se obtiene, asimismo, manteniendo constantes las cotas de dos cualesquiera de sus puntos, tales como M y N; resultando el segmento M’’1 N’’1 como nueva proyección vertical de la recta.
Paso 2- El punto intersección I’’1, obtenido en la proyección auxiliar, se traslada siguiendo las direcciones de proyección entre vistas para determinar I’ y I’’ como proyecciones horizontal y vertical del punto intersección, en sus vistas diédricas iniciales.
r ∩ ¬ABC → I
INTERSECCIÓN DE DOS PLANOS DADOS POR TRES PUNTOS
Método del plano de corte proyectante
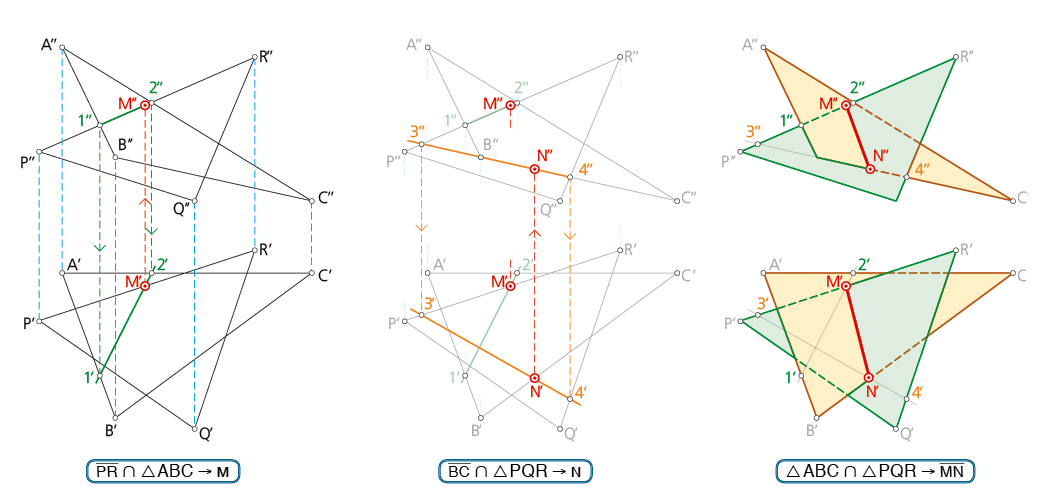
Se parte de conocer la proyección vertical (alzado) y la correspondiente proyección horizontal (planta) de los planos ABC y PQR y se requiere determinar la recta intersección entre ellos por medio de planos de corte proyectantes.
El método consiste en hallar dos puntos de la recta común a ambos planos; los cuales se obtienen mediante la intersección de una recta perteneciente a uno de ellos con el otro, por partida doble.
• Paso 1 - En la ilustración se ha determinado el punto M como intersección de la recta PR perteneciente al plano PQR con el plano ABC.
• Paso 2 - Análogamente, el punto N es la intersección de la recta BC, perteneciente al plano ABC, con el plano PQR. El segmento MN define la recta común de los planos considerados. El proceso seguido es idéntico al para determinar un punto intersección de una recta con un plano siendo, en la ilustración que nos ocupa, mas adecuado usar planos proyectantes verticales (de canto).
• Paso 3 - Una vez determinados los dos puntos M(M’-M’’) y N(N’-N’’) y con ello el segmento MN común a los dos planos, se hace necesario determinar las partes vistas u ocultas de cada uno de ellos. Las partes vistas y ocultas en cada proyección, se consigue con el análisis de las distancias relativas en la zona común.
r ∩ ¬ABC → I
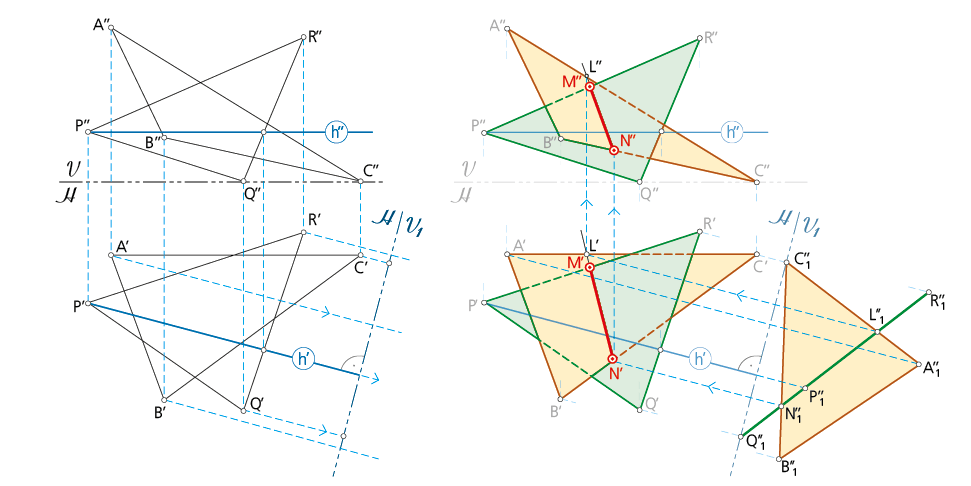
Método de la vista auxiliar
Se parte de conocer las vistas alzado y planta de dos planos ABC y PQR respectivamente (los mismos que se han planteado para explicar el método anterior); y lo que se desea es determinar la recta intersección entre ambos directamente. Para lograrlo se crea una vista auxiliar que conduzca a uno de los planos (en la figura el correspondiente al triángulo PQR), a proyectarse como un plano proyectante vertical (de canto). El plano ABC, condicionado por la nueva proyección vertical, dibuja la proyección A’’1B’’1C’’1 conservando todos sus puntos las cotas iniciales. En esta vista auxiliar, la vista de canto de PQR atraviesa al plano ABC por los puntos L y N. Trasladados dichos puntos a las vistas iniciales (primero sobre la planta y después sobre el alzado) se obtiene la recta intersección entre los planos en su posición inicial. Por último, se visualizan las partes vistas y ocultas de cada proyección diédrica.