
4.1 Fundamentos.
En la resolución de los problemas de perpendicularidad se han de tener en cuenta los siguientes principios geométricos.
SISTEMA DIÉDRICO
Unidad 7
La relación de perpendicularidad puede darse entre dos rectas; dos planos o entre una recta y un plano.
En proyecciones diédricas, en contra de lo que sucede en paralelismo, dos rectas o dos planos que son perpendiculares, no guardan relación singular entre sí; es decir, que la perpendicularidad no se conserva en el paso del espacio a la proyección.

En la resolución de los problemas de perpendicularidad se han de tener en cuenta los siguientes principios geométricos.
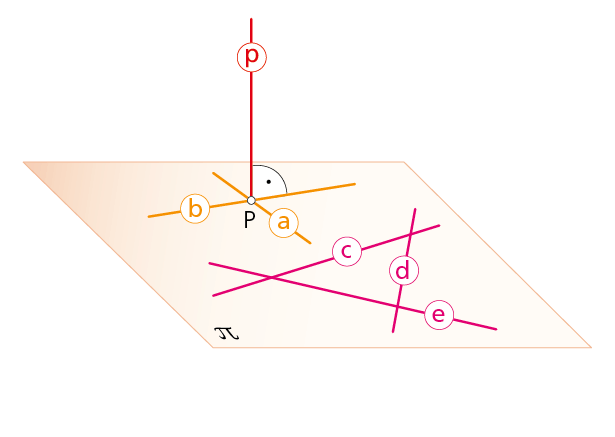
«Si dos rectas son perpendiculares en el espacio –cruzándose o cortándose– y una de ellas es paralela a un plano, las proyecciones ortogonales de las dos rectas, sobre dicho plano, son perpendiculares entre sí».
Las rectas a y b son perpendiculares entre sí y, por consiguiente, los planos α y β que las contienen serán perpendiculares entre sí, siendo, asimismo, perpendiculares al plano π como ves en la imagen inferior.
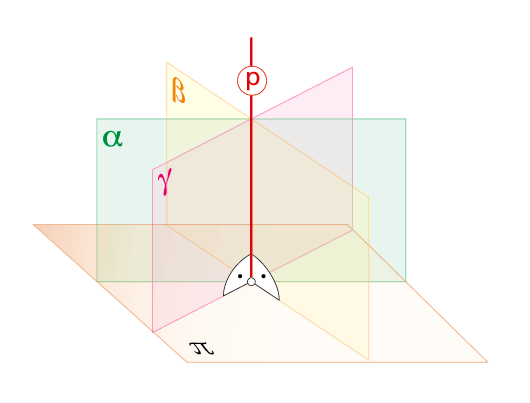
Si una recta es perpendicular a un plano, también lo es a todas las infinitas rectas contenidas en él».
La recta p es perpendicular al plano π y, por tanto, también a las rectas a, b, c, d,…En definitiva, dos rectas, p y e por ejemplo, serán perpendiculares si por una de ellas se puede trazar un plano α perpendicular a la otra.
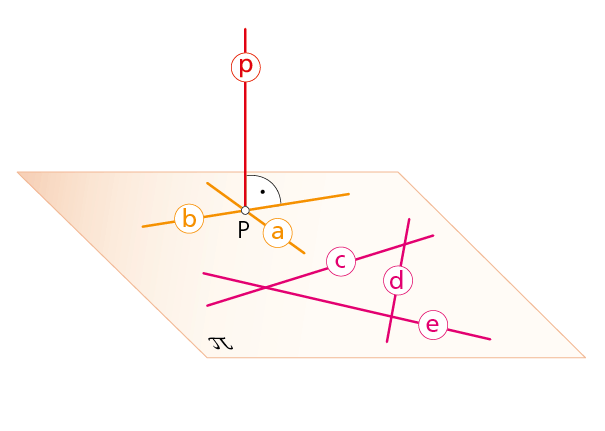
«Un plano a, b... será perpendicular a otro π, cuando contenga a una recta p perpendicular al mismo».Recíprocamente, el plano π será perpendicular a otros (α, β, g, …) cuando lo sea a su recta intersección (p)». Todos los planos del haz que pasan por su recta común p son perpendiculares al plano π, y viceversa..
Como se ha dicho anteriormente, si una recta r es perpendicular a un plano α, será necesariamente perpendicular a todas las rectas contenidas en α y, por consiguiente, a su traza α1; por ello, la proyección r’ de la recta será perpendicular a la traza α1 del plano. Idéntico razonamiento puede hacerse con respecto al plano vertical de proyección. Por tanto, si el sistema diédrico trabaja, básicamente, con los dos planos de proyección (H y V) puede enunciarse la siguiente conclusión: «Para que una recta sea perpendicular a un plano ha de verificarse que las proyecciones de la recta sean perpendiculares a las trazas homónimas del plano». Así, si por un punto P se traza una recta r perpendicular al plano α, será suficiente con dibujar por P’ y P’’ las proyecciones r’ y r’’ perpendiculares a las trazas del plano.
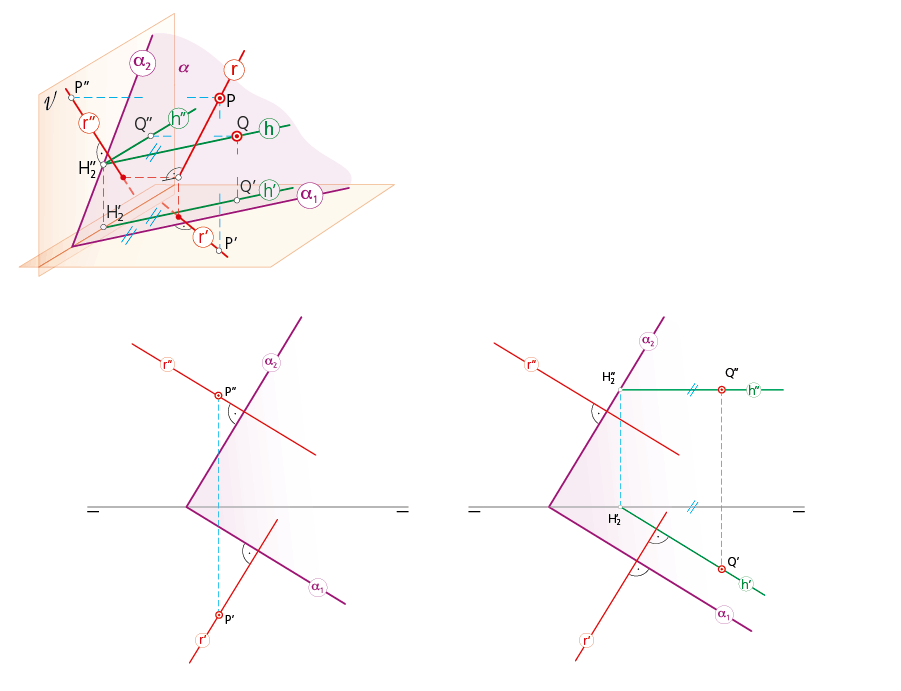
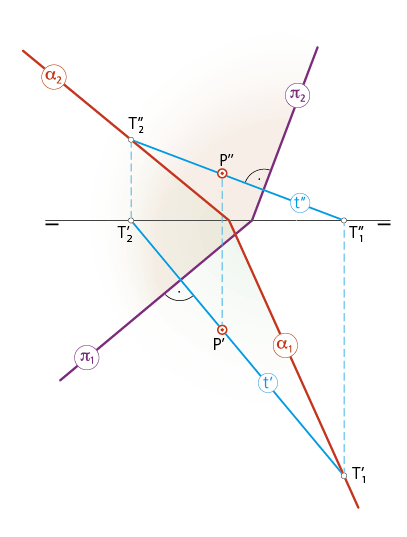
De acuerdo a lo dicho en la fig. 4.1.c, el plano α será perpendicular a otro π cuando uno de ellos, por ejemplo el α, contenga a una recta (i) perpendicular al otro. Por consiguiente, todos los planos que pasen por la recta i serán perpendiculares a π, de ahí que existan infinitas soluciones. En la imagen inferior, para trazar por el punto P un plano a perpendicular a otro π dado, se comienza por dibujar, por dicho punto, una recta t (t’-t’’) perpendicular a π. Cualquier plano tal como el α, cuyas trazas pasen por los puntos traza de la recta t (esto es, por T1 y T2 respectivamente), será perpendicular al plano π dado.