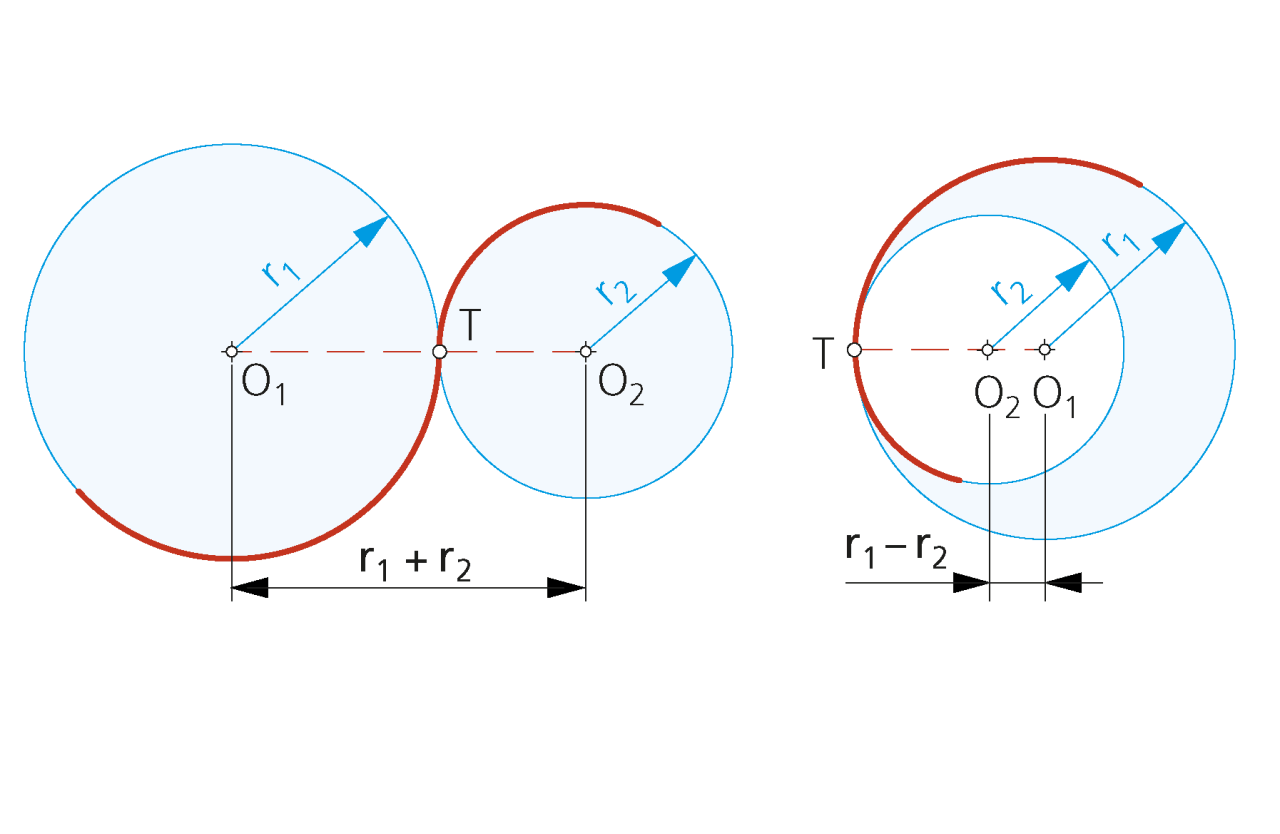TANGENCIAS Y CURVAS TÉCNICAS
Unidad 4
1- TANGENCIAS
Las tangencias son trazados geométricos presentes en numerosos diseños, estructuras arquitectónicas e infinidad de formas decorativas y objetos de uso común.
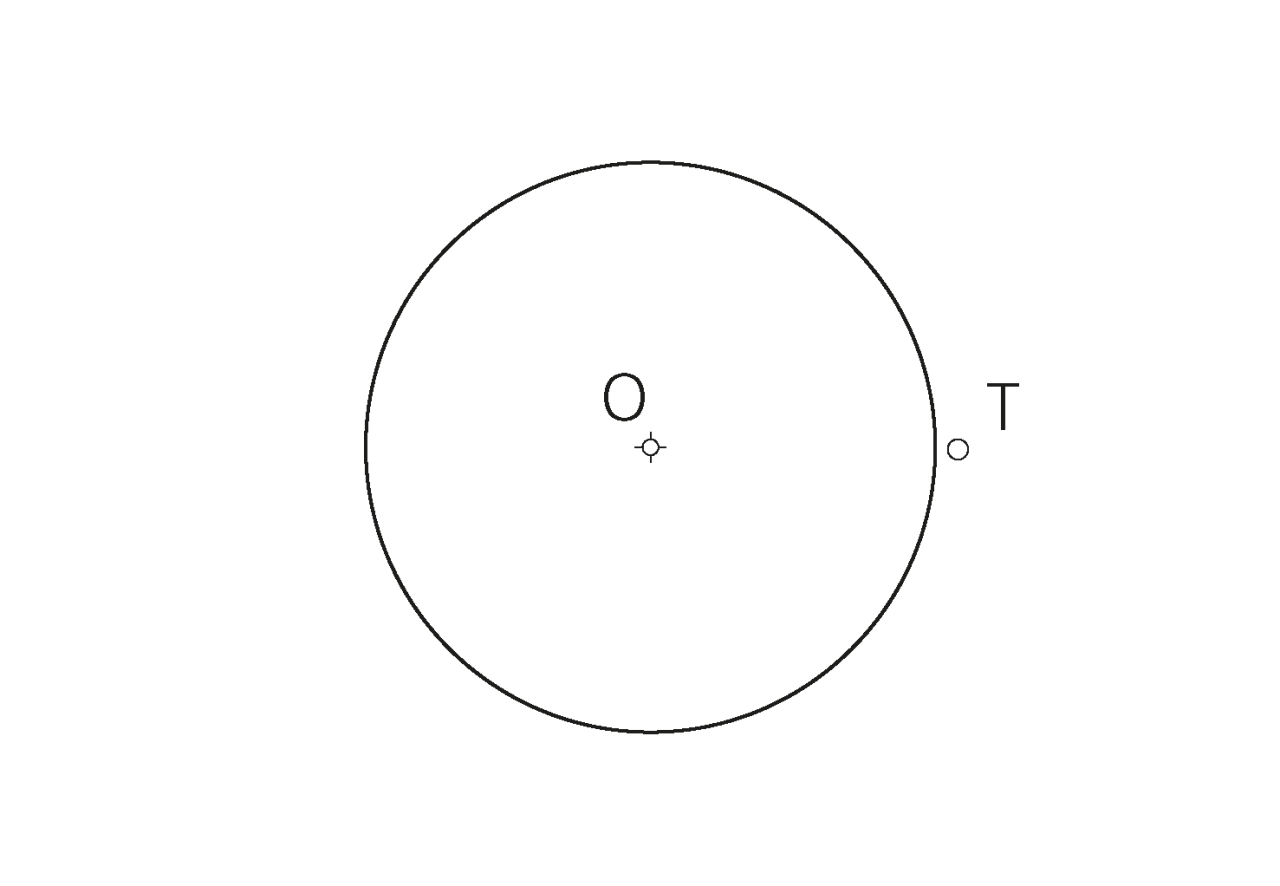
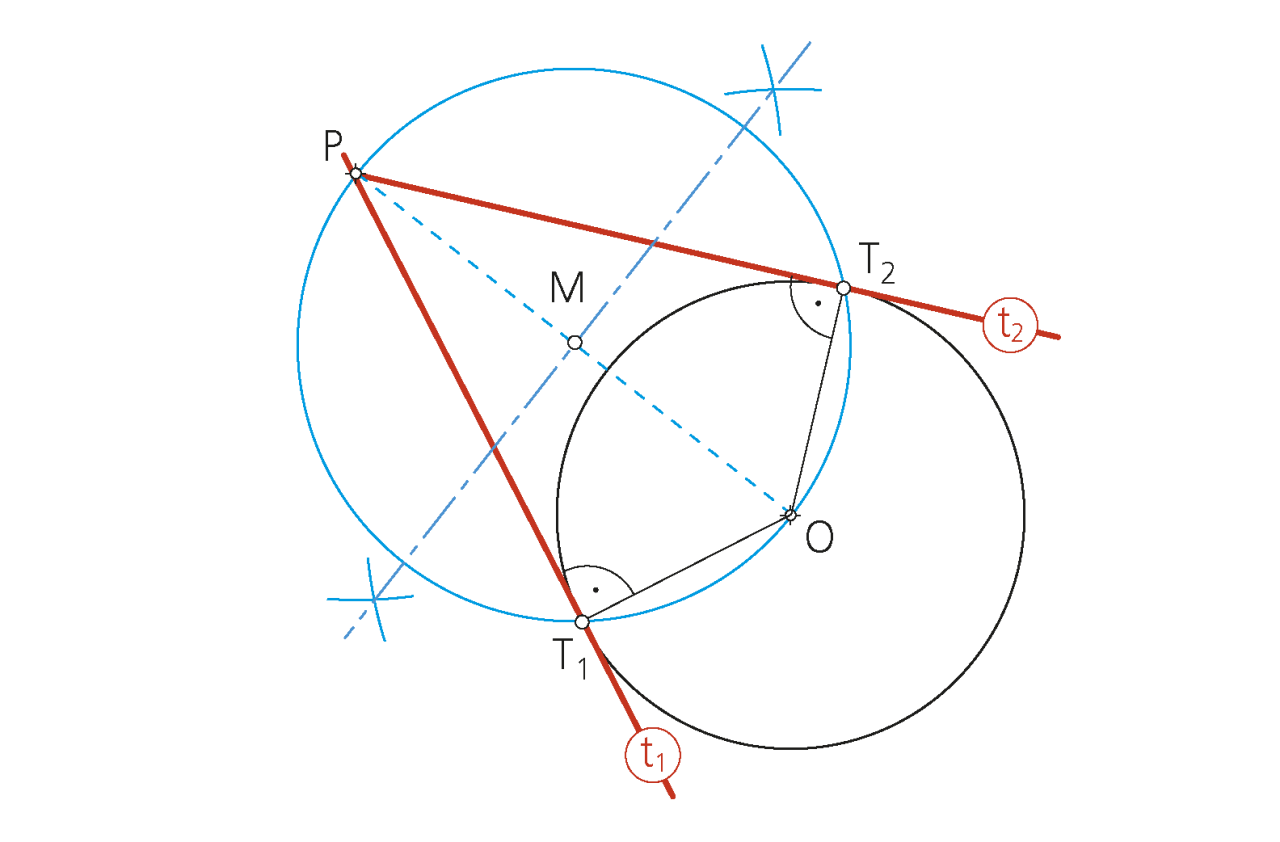
Recordemos que dos líneas se dice que son tangentes cuando tienen un solo punto común sin cortarse. Este punto de tangencia es el que permite el enlace o transición suave de una línea a otra sin brusquedad alguna. Para resolver cualquier problema de tangencias de rectas con circunferencias y de estas entre sí, es necesario aplicar con todo rigor las propiedades o principios geométricos fundamentales que a continuación se indican.
1.1 Propiedades fundamentales
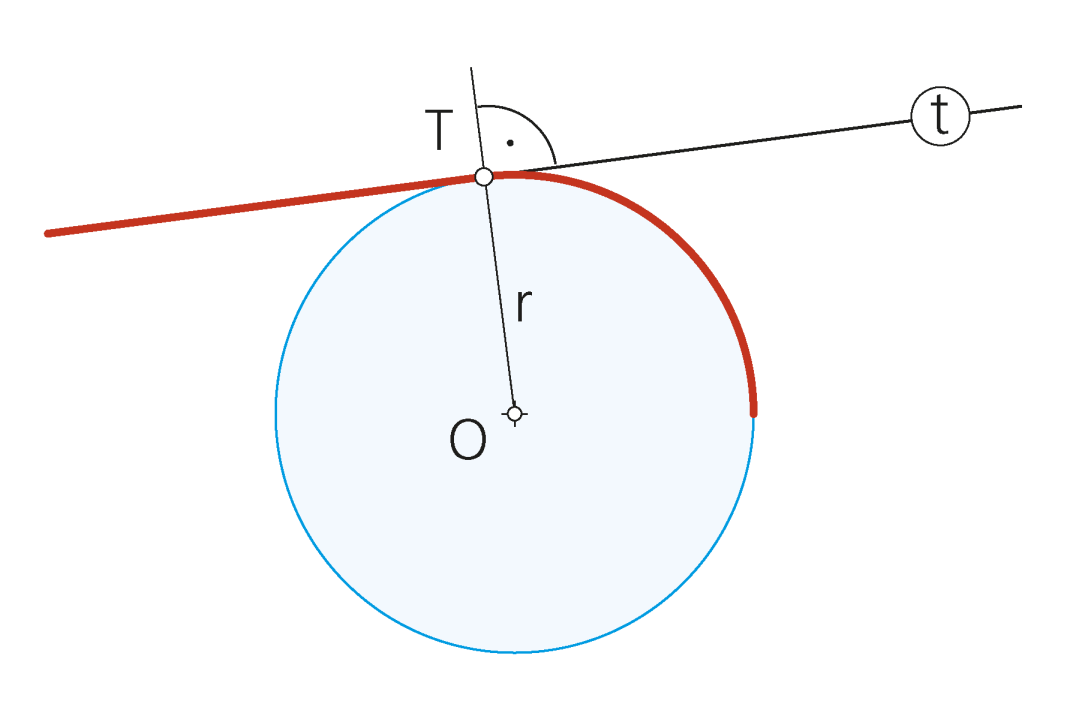
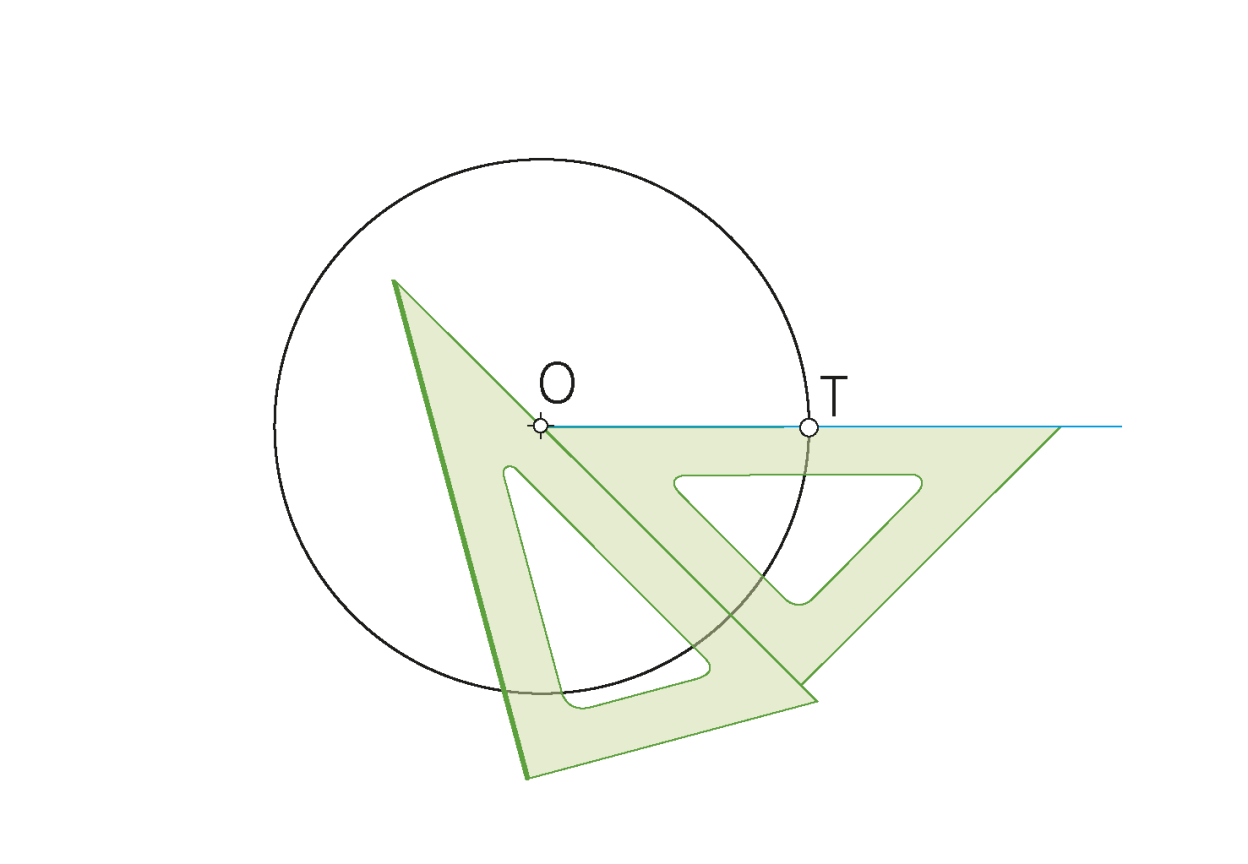
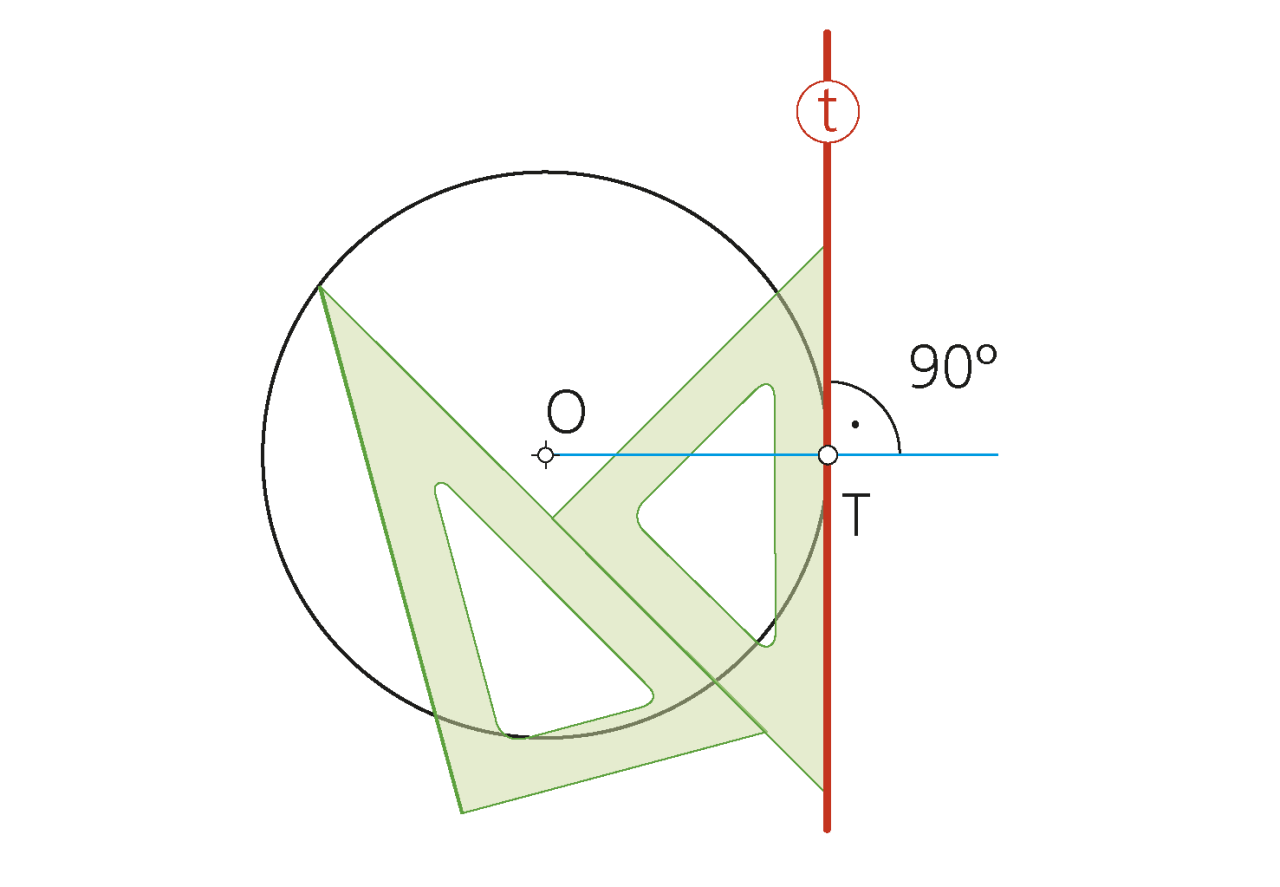
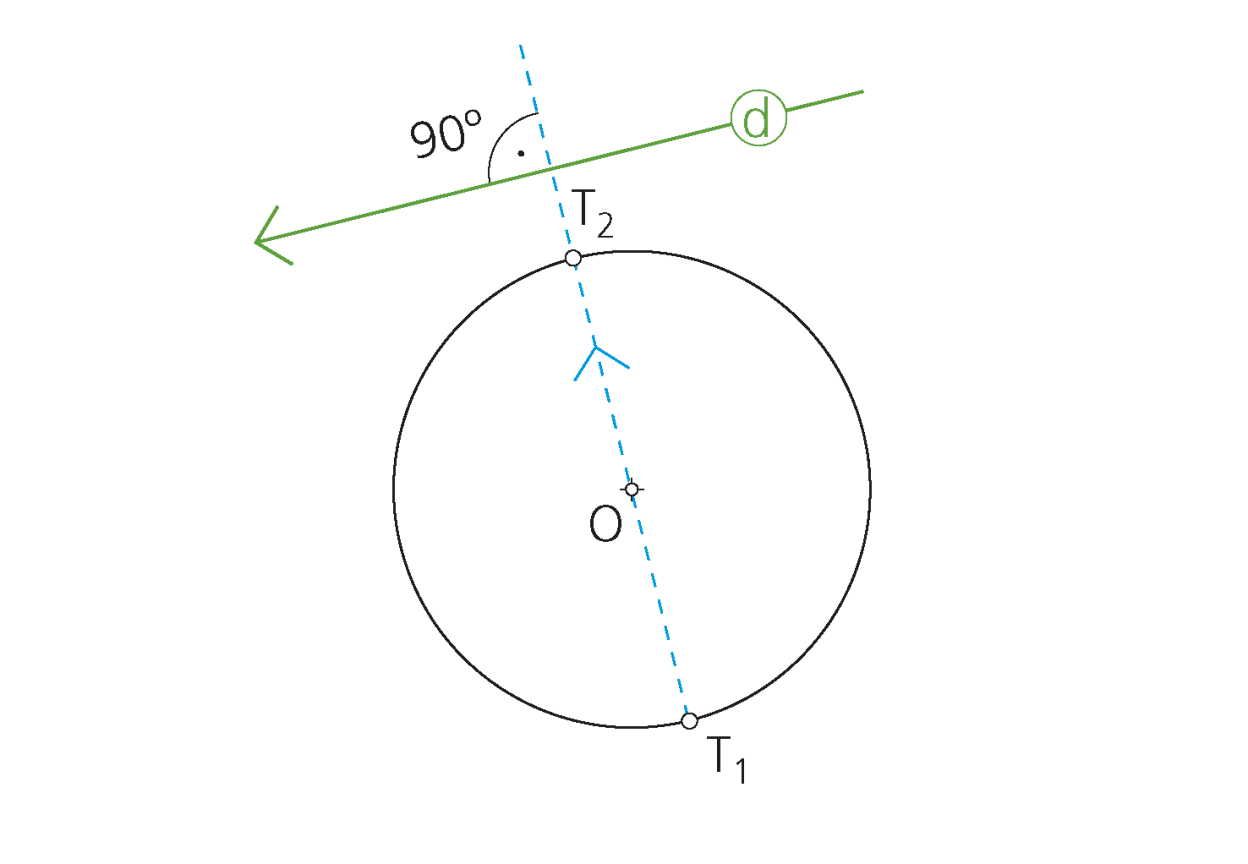
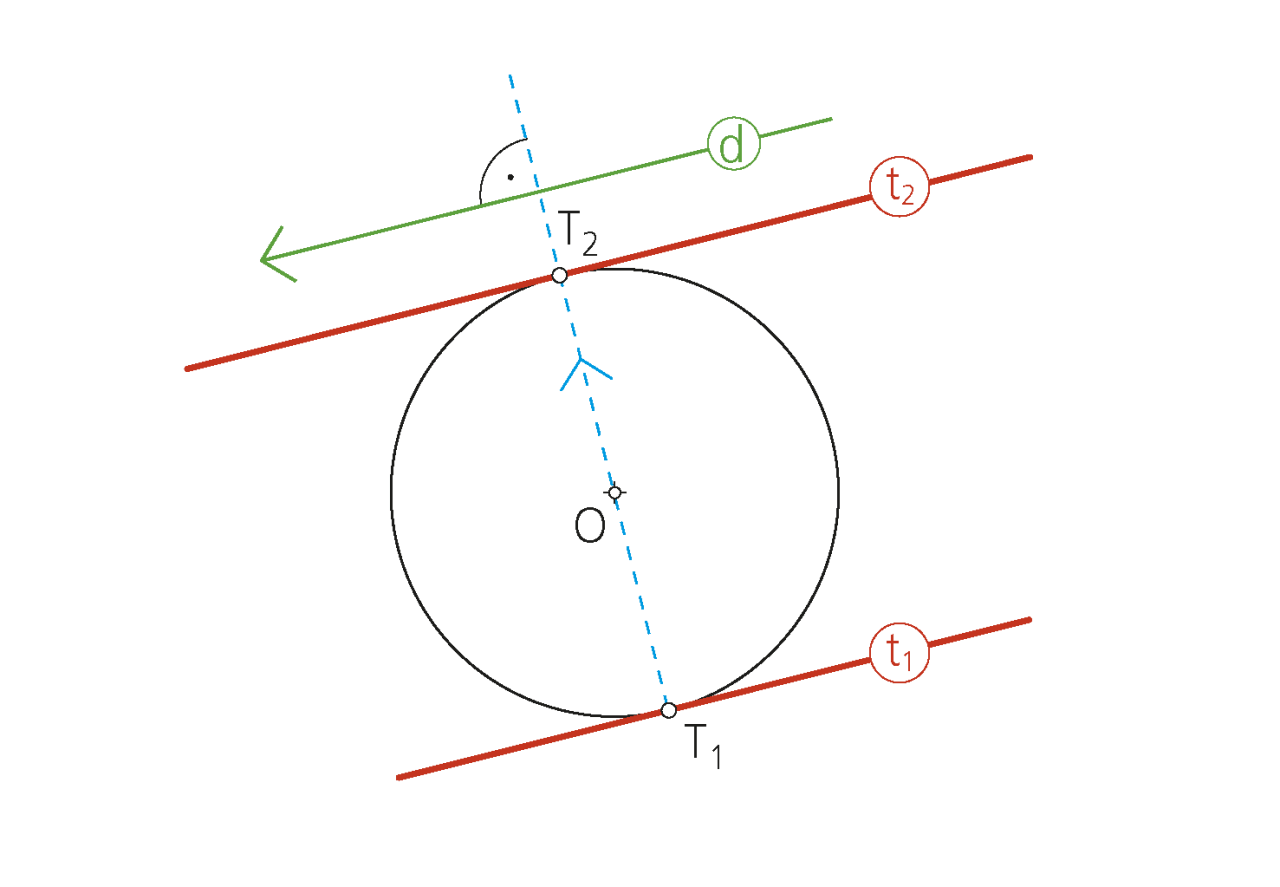
«Si una recta es tangente a una circunferencia, el radio en el punto de tangencia es perpendicular a la recta».
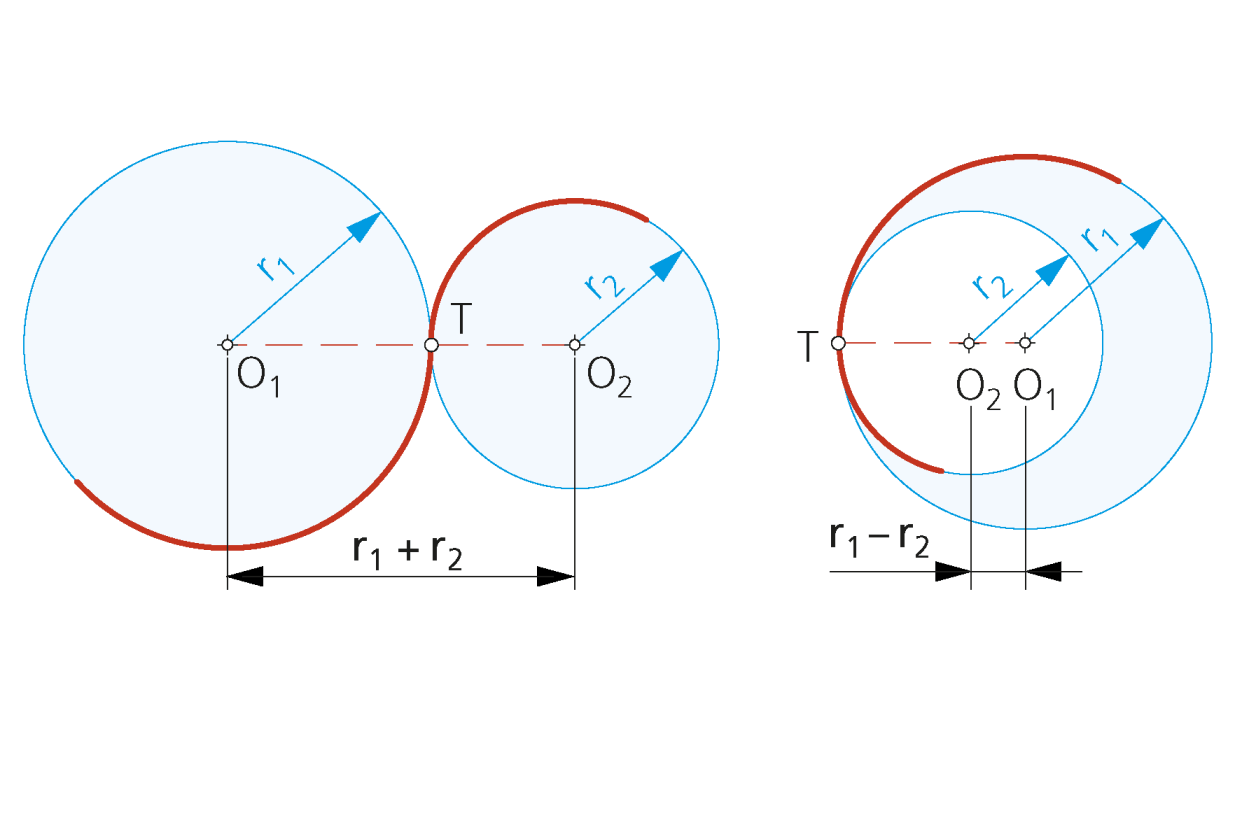
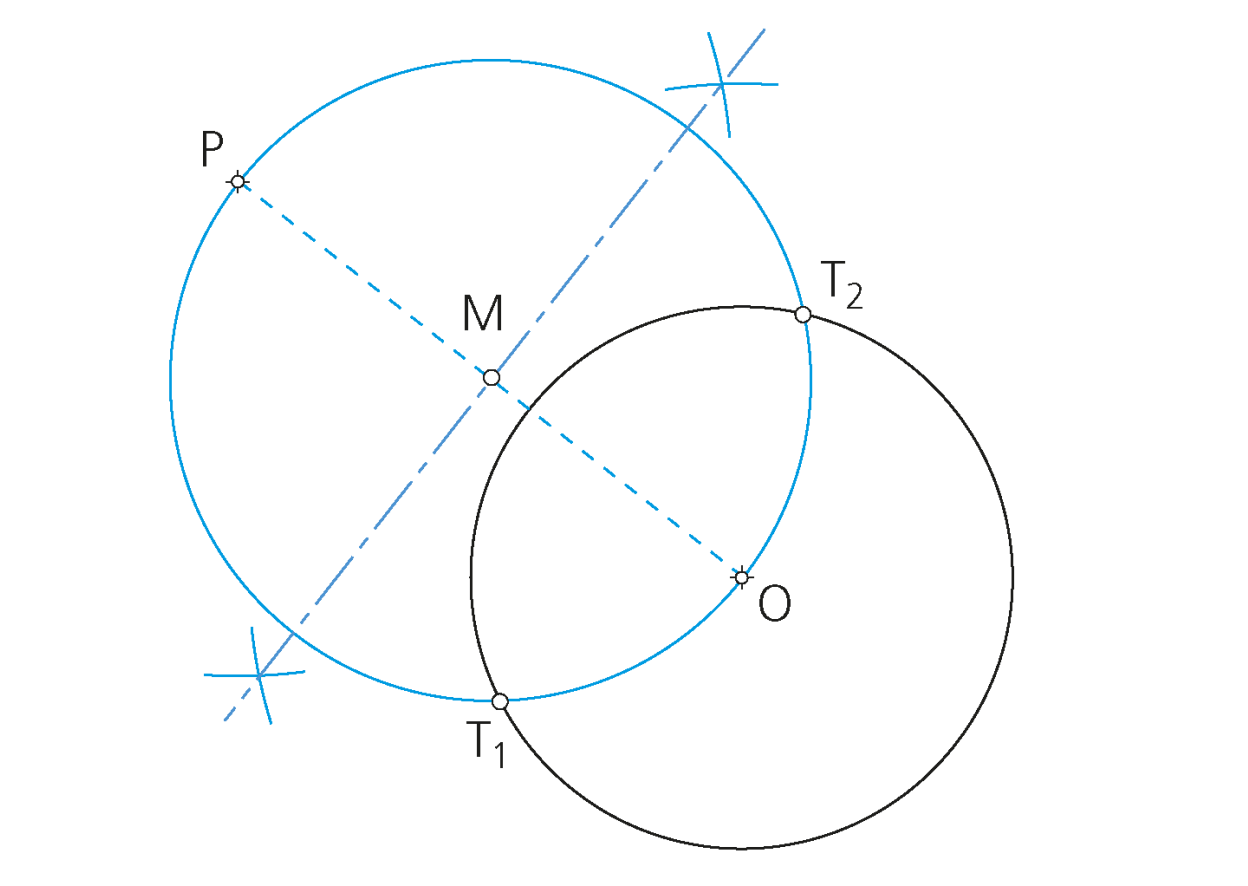
«Si dos circunferencias son tangentes (exteriores e interiores), sus centros están alineados con el punto de tangencia y distan la suma de sus respectivos radios».
1.2 Consideraciones Geométricas
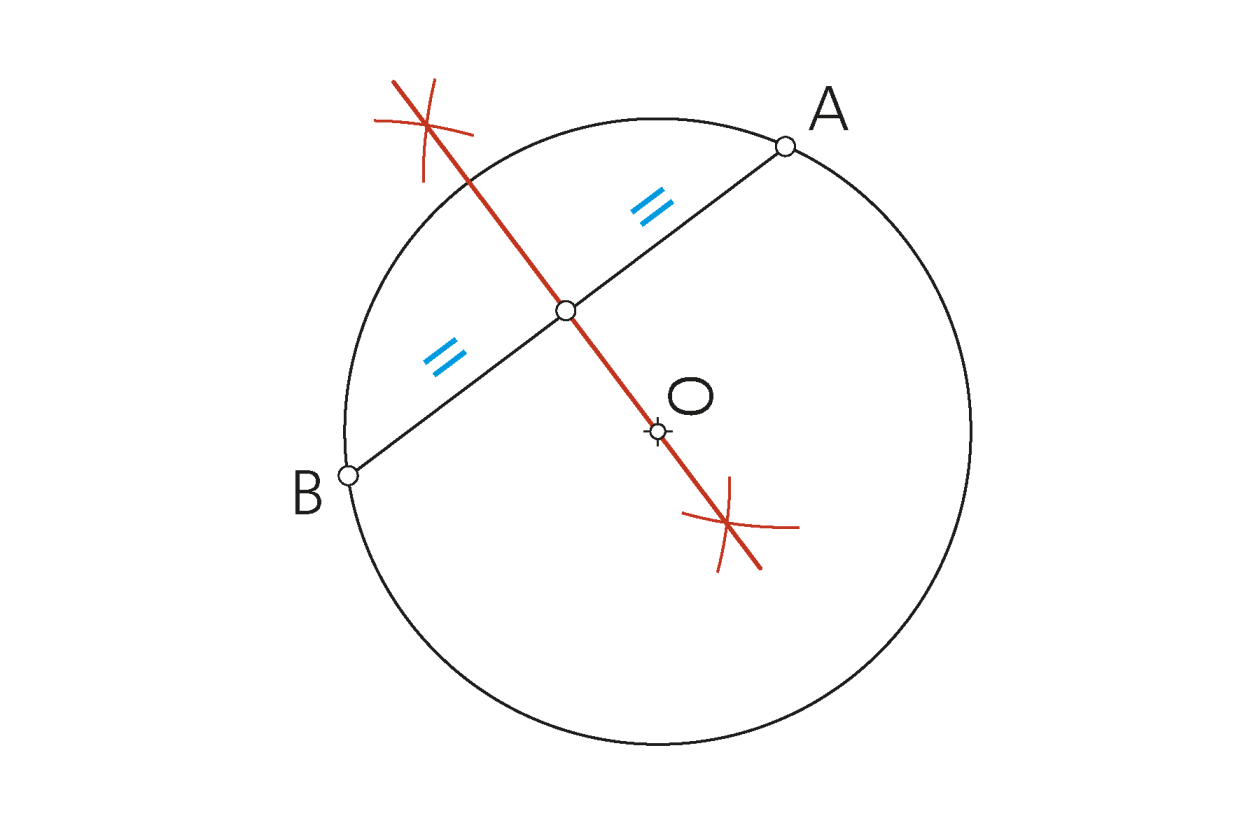
«El centro de una circunferencia que pasa por dos puntos A y B se encuentra en la mediatriz del segmento que los une».
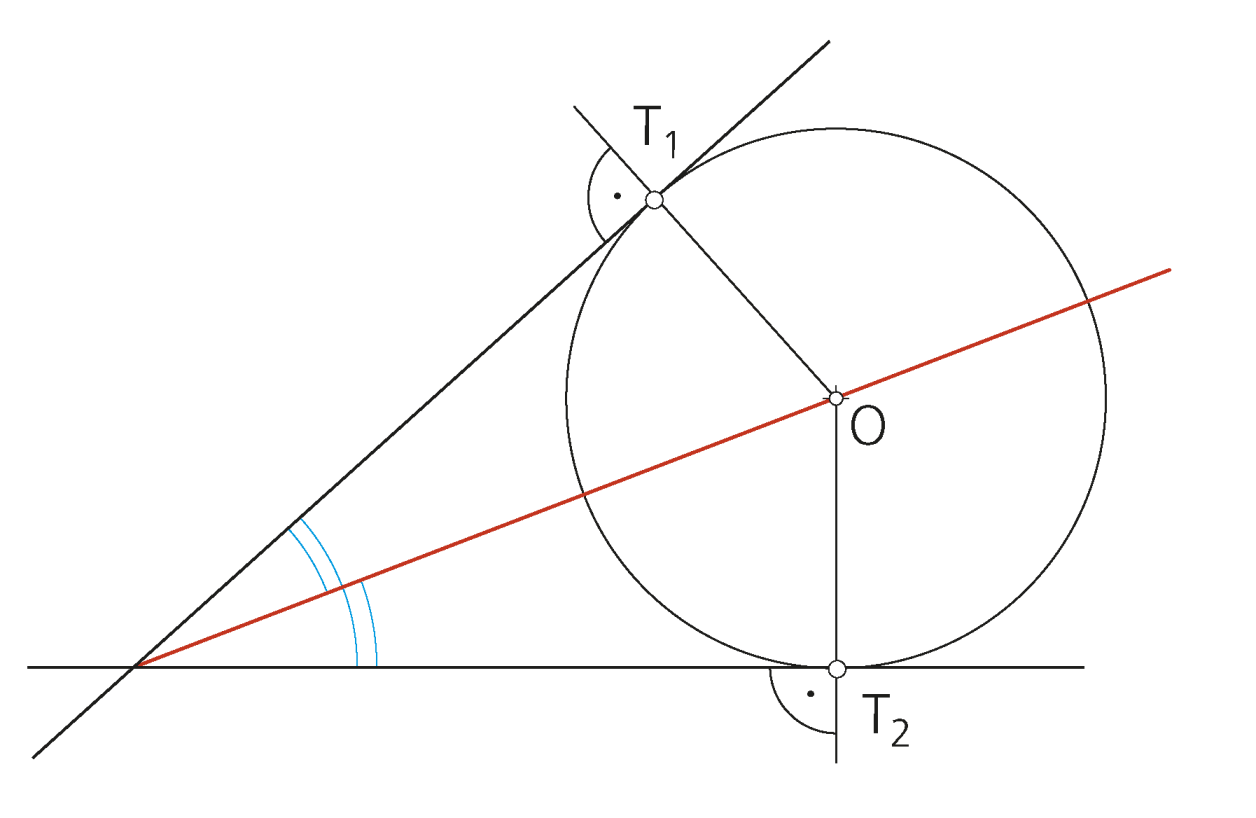
«Si una recta es tangente a una circunferencia, el radio en el punto de tangencia es perpendicular a la recta».
TRAZADO DE RECTAS TANGENTES A UNA CIRCUNFERENCIA
Por un punto T de la circunferencia
Datos:• Circunferencia de centro O.• Punto T de ella.
Se traza el radio OT alineando la escuadra según indica la figura.
Girando la escuadra trazamos por T la recta tangente solución.
Paralelas a una dirección d
Datos: • Circunferencia de centro O.
• Dirección: d.
Por el centro O trazamos la perpendicular a la dirección d, obteniendo los puntos de tangencia T1 y T2.
Por los puntos T1 y T2 trazamos paralelas a la dirección d, obteniendo las rectas tangentes t1 y t2.
Por un punto P exterior a la circunferencia
Datos:
• Circunferencia de centro O.
• Punto exterior P.
Se traza la mediatriz del segmento PO para obtener el punto M, centro de la circunferencia, de igual diámetro que el segmento, que corta a la dada en T1 y T2, puntos de tangencia de las rectas solución.
La unión de los puntos T1 y T2, con el punto exterior P define las dos rectas tangentes t1 y t2 que es posible trazar desde un punto exterior a una circunferencia.
TRAZADO DE RECTAS TANGENTES EXTERIORES A DOS CIRCUNFERENCIAS
Circunferencia de centro O1 y O2, con radios r1 y r2 respectivamente.
Con centro en la circunferencia de radio (02), se dibuja la circunferencia de radio la diferencia de las dadas.
Desde el centro de la circunferencia de menor radio (01), se trazan las tangentes a la circunferencia diferencia de radios (r2 - r1) obteniendo los puntos 1 y 2. La prolongación de los radios O2 1 y O2 2 define los puntos de tangencia T1 y T2.
Las rectas t1 y t2, tangentes solución, contactan en T1 y T2 y son paralelas a las tangentes antes obtenidas. Los puntos de contacto T3 y T4 son los pies de las perpendiculares trazadas por O1 a las tangentes solución.
TRAZADO DE RECTAS TANGENTES INTERIORES A DOS CIRCUNFERENCIAS
Datos:
• Circunferencia de centro O.
• Punto exterior P.
Se traza la mediatriz del segmento PO para obtener el punto M, centro de la circunferencia, de igual diámetro que el segmento, que corta a la dada en T1 y T2, puntos de tangencia de las rectas solución.
La unión de los puntos T1 y T2, con el punto exterior P define las dos rectas tangentes t1 y t2 que es posible trazar desde un punto exterior a una circunferencia.
1.3 Aplicaciones de tangencias en la vida diaria
En el día a día podemos encontrar una gran cantidad de tangencias, enlaces y curvas técnicas aplicadas en objetos de uso común; tales como un vaso, una bombilla o una silla, como muestran los ejemplos. También podemos ver tangencias en la cadena de una bicicleta, el arco de una puerta, un grifo, el diseño de una farola... Observa en tu entorno en el aula o en tu habitación si puedes encontrar algún ejemplo de tangencia (lo más fácil) o espiral (un poco más difícil). Los objetos decorativos como azulejos en las paredes, molduras de yeso en los techos o marcos de cuadros son un buen lugar para buscar estos ejemplos.
Ejemplos
