TANGENCIAS Y CURVAS TÉCNICAS
+ CONTENIDO COMPLEMENTARIO
Unidad 4
TRAZADO DE CIRCUNFERENCIAS TANGENTES DE LADO CONOCIDO
Por un punto T de una recta t.
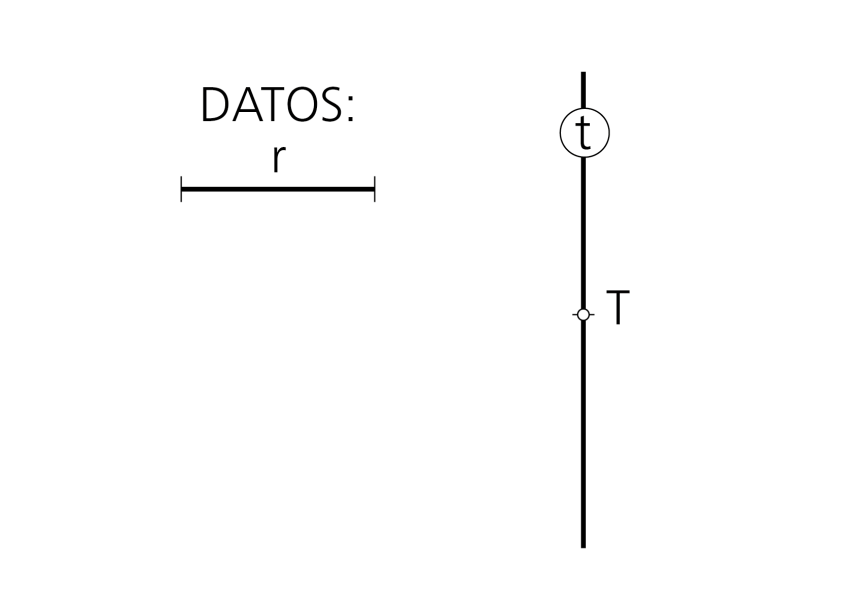
Datos: Recta t y punto T de ella, así como la magnitud r del radio de las circunferencias solución.
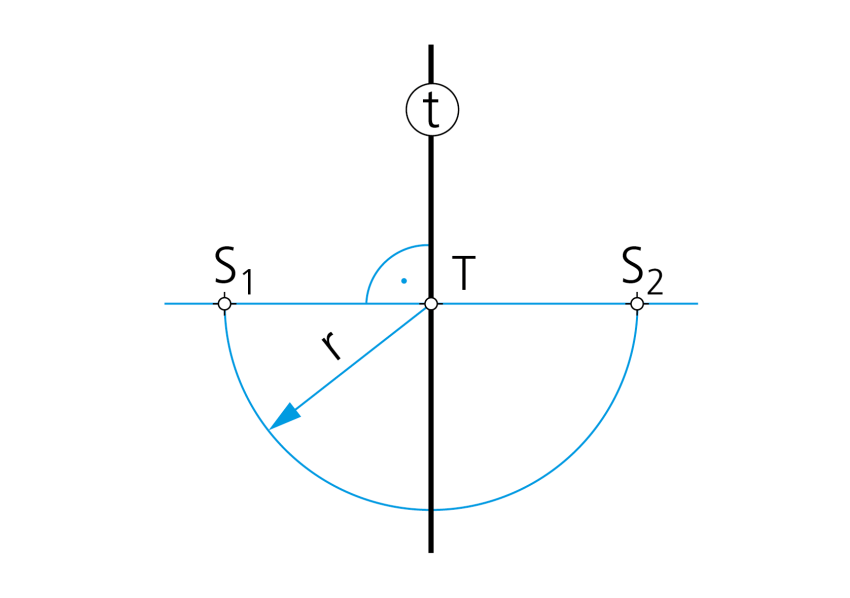
Paso 1- Se traza la perpendicular a la recta t por el punto T y se lleva el radio r en los dos sentidos, obteniendo así los puntos S1 y S2, centros de las dos posibles soluciones.
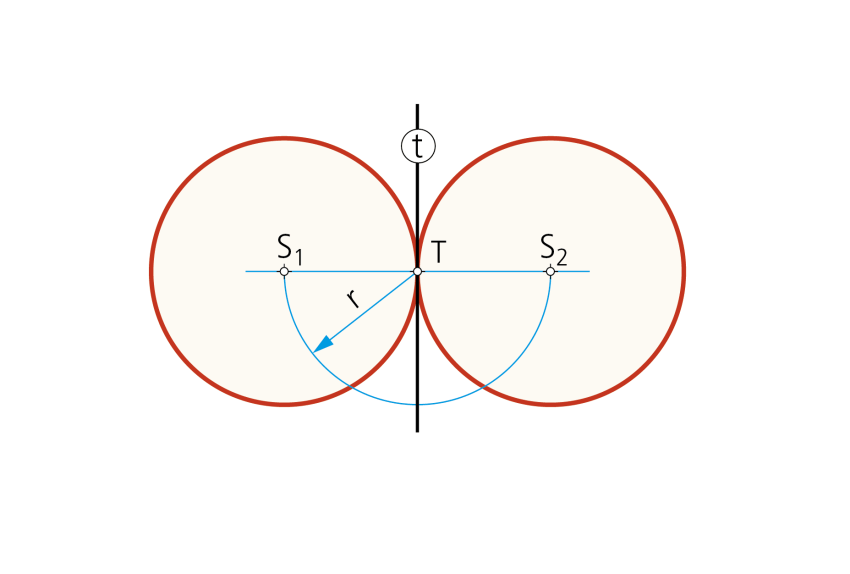
Paso 2- Con centro en S1 y S2 y radio r se obtienen las dos circunferencias tangentes a la recta t en el punto T.
A una recta M pasando por un punto exterior P.
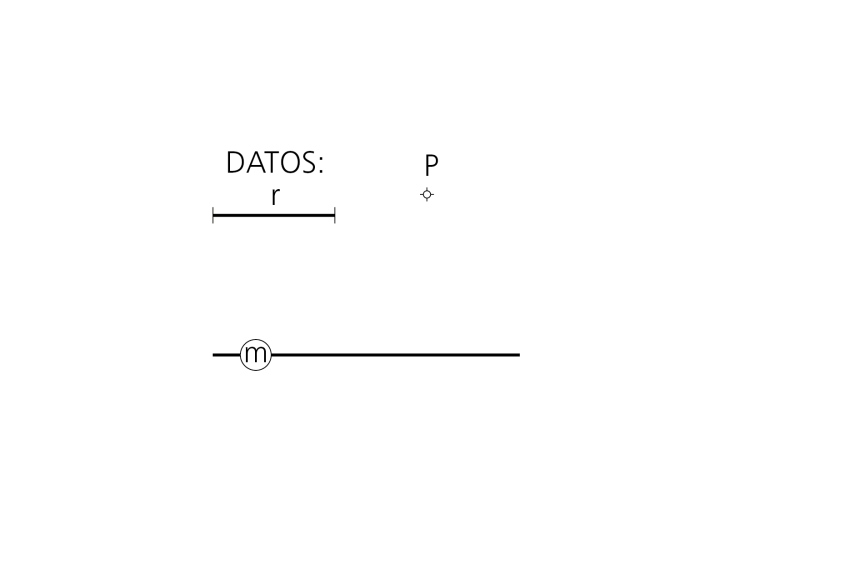
Datos: Recta m, punto P y radio.
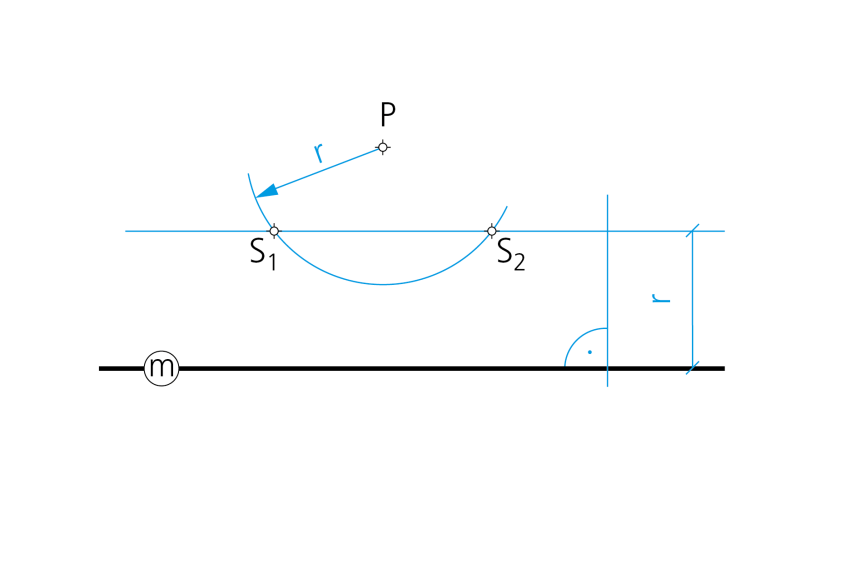
Paso 1-- Dado que la circunferencia solución ha de pasar por P y ser tangente a la recta m, su centro equidistará (l.g.) de ambos elementos. Por ello, y para su localización, se traza la paralela a m distante la magnitud r, y con centro en P un arco de radio r; los puntos de intersección S1 y S2 son los centros de las circunferencias solución.
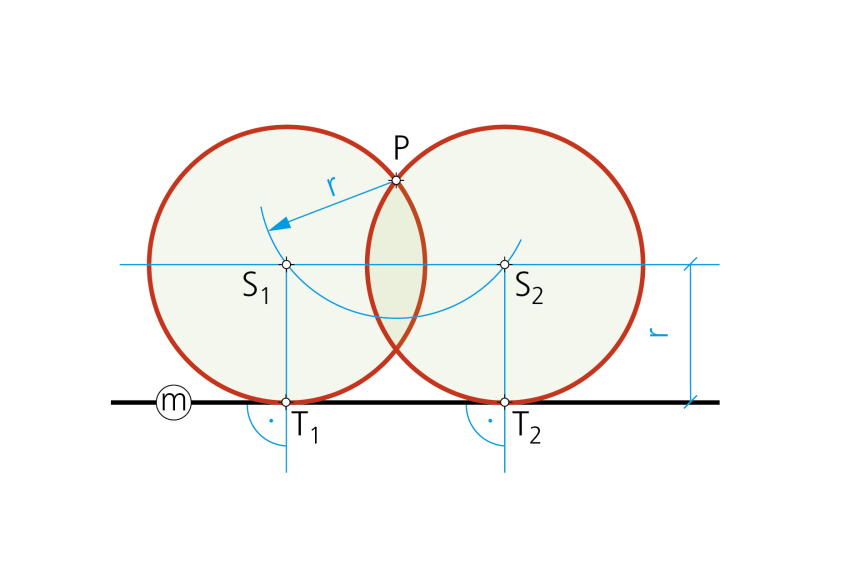
Paso 2- Se trazan las dos circunferencias y se definen los puntos de tangencia T1 y T2 con la recta.
A dos rectas a y b que se cortan

Datos: Rectas a y b. Radio r de las circunferencias solución. Rectas a y b. Radio r de las circunferencias solución.

Paso 1- Recordando la segunda consideración geométrica anunciada al comienzo de esta unidad didáctica, el centro de las circunferencias tangentes (siendo posibles cuatro soluciones) se encuentran en las bisectrices de los ángulos que forman las rectas a y b dadas. Asimismo, los centros distarán una magnitud r de cada recta. Los puntos comunes a ambos lugares geométricos determinan los centros S1 y S2.
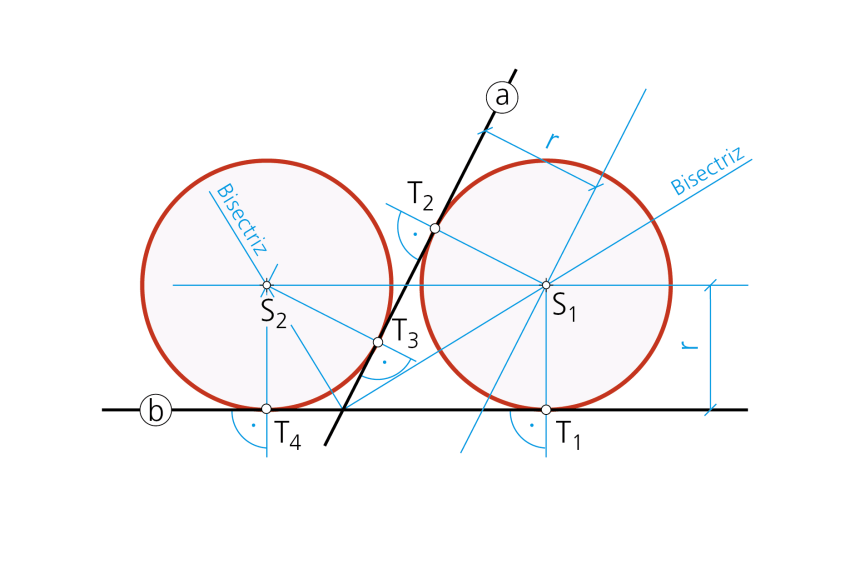
Paso 2- Se han dibujado únicamente dos soluciones. Las otras dos son las simétricas respecto al ángulo del vértice que forman las rectas a y b. Los puntos T1, T2, T3 y T4 son los de tangencia de las correspondientes soluciones.
A una circunferencia de centro O por un punto T de ella.
Por un punto T de una recta t.
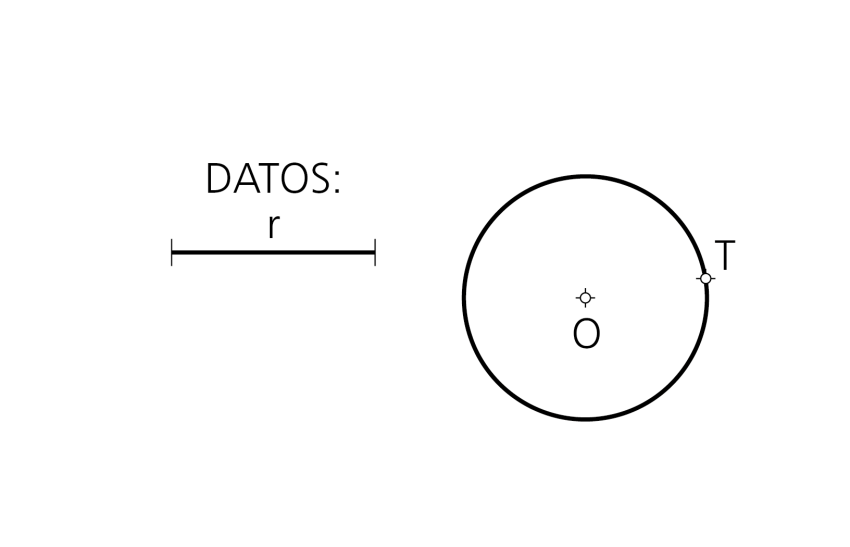
Datos: Circunferencia de centro O, punto P y radio r de las circunferencias tangentes pedidas.
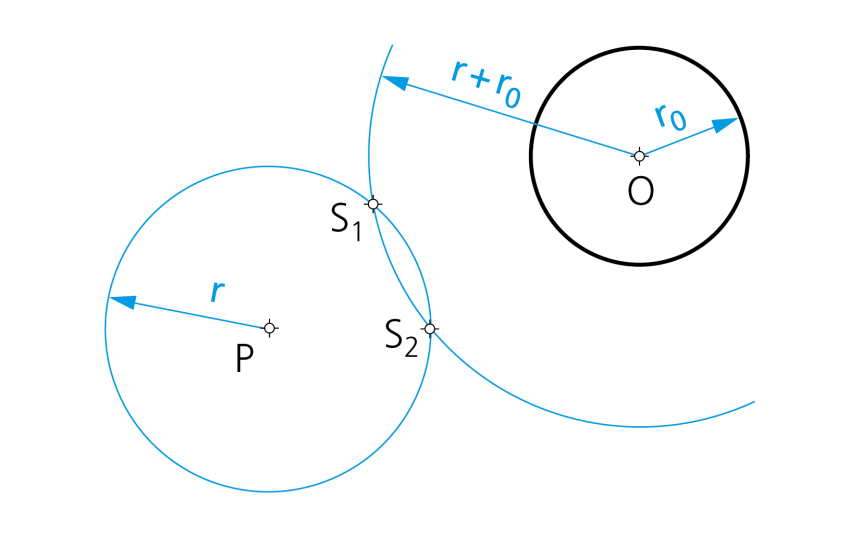
Paso 1- Los centros de las circunferencias solución, son puntos que han de equidistar (lugares geométricos) de la circunferencia dada y del punto P. Por ello, se encontrarán en la intersección de la circunferencia de radio r y centro P con la de centro O y radio r + r0.
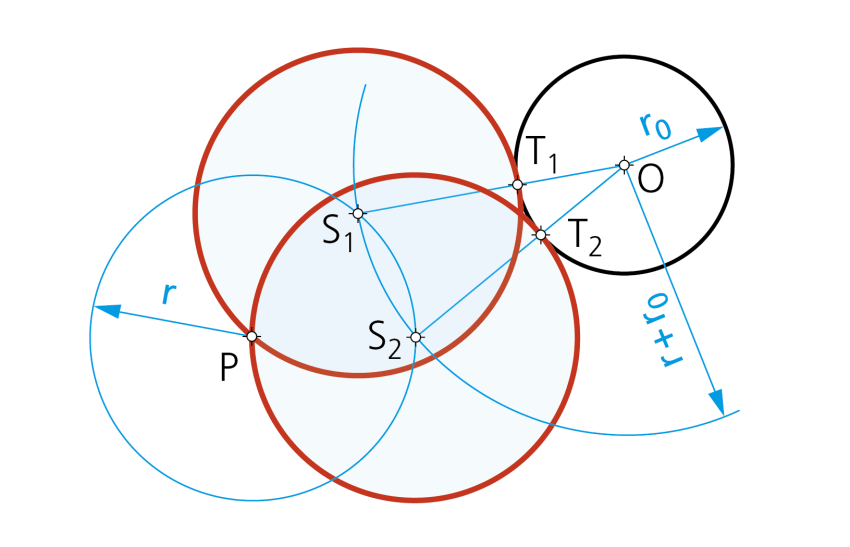
Paso 2- Con centro S1 y S2 se dibujan las dos circunferencia solución.
TRAZADO DE CIRCUNFERENCIAS TANGENTES DE LADO DESCONOCIDO
A una recta t en un punto T de ella y que pasa por otro exterior P.
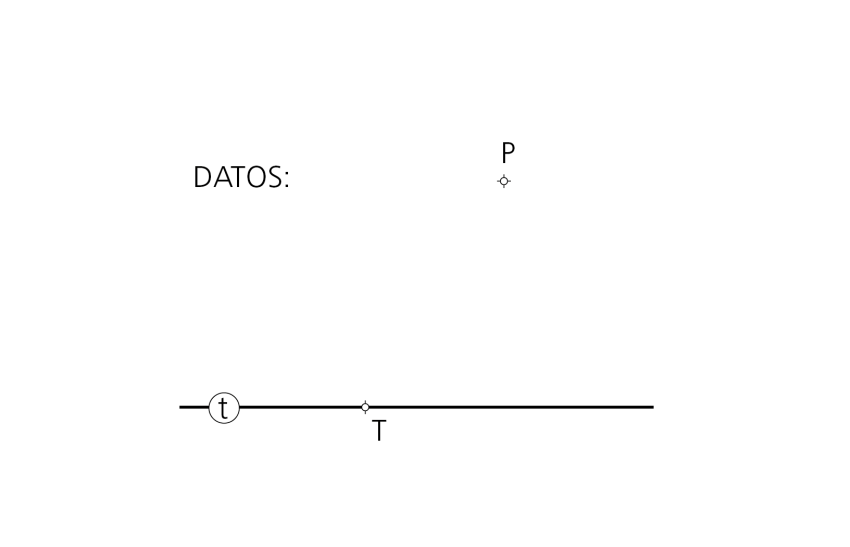
Datos: : Recta t y punto T en la recta y P exterior a ella.
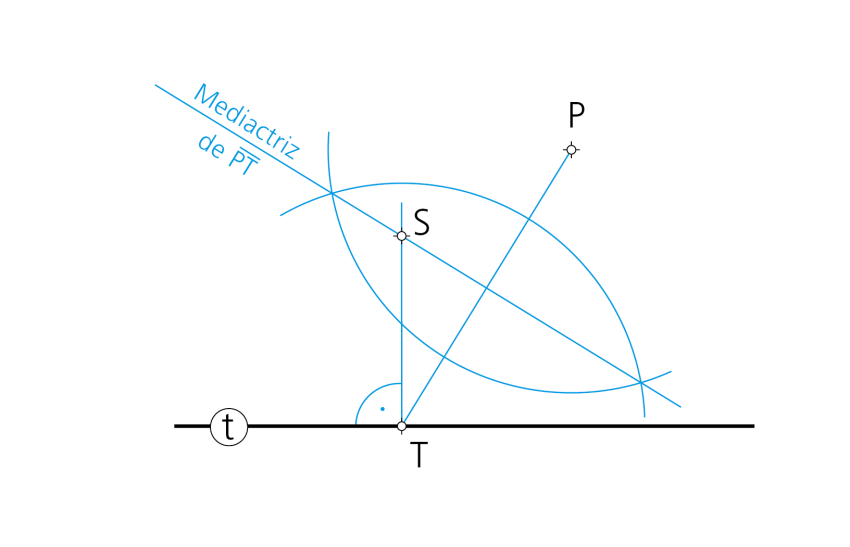
Paso 1- El problema admite una única solución: la circunferencia que tiene como centro el de la intersección de la perpendicular por T y la mediatriz del segmento PT.
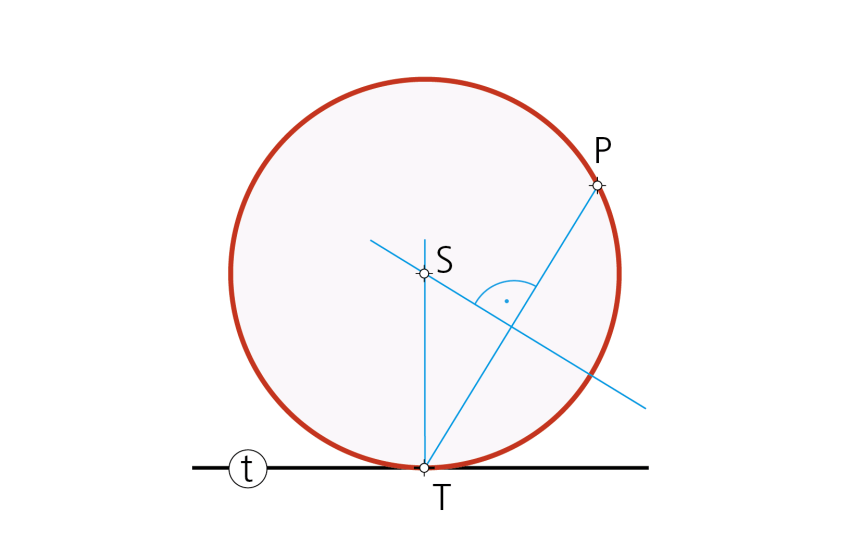
Paso 2- El radio de la circunferencia solución es la que se obtiene con centro en S y radio ST, como indica la figura.
A dos rectas y que pasen por un punto T.
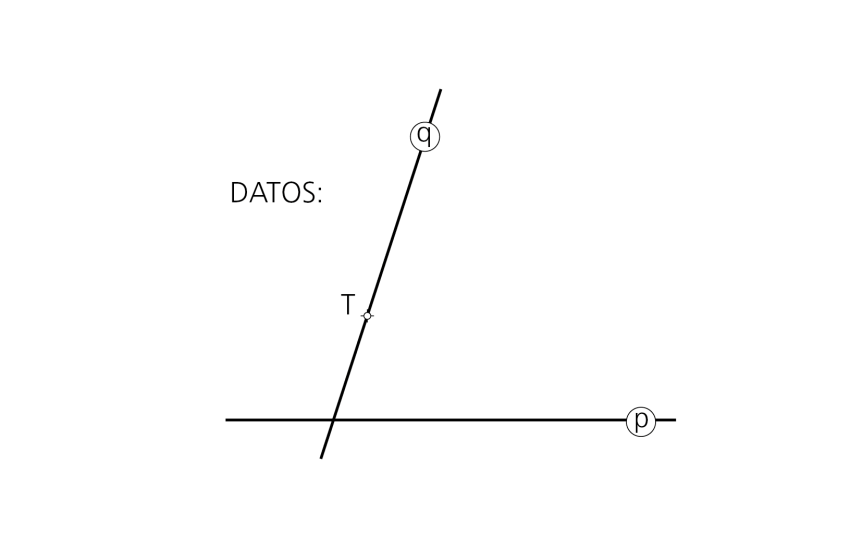
Datos: Rectas p y q y punto T sobre ellas.
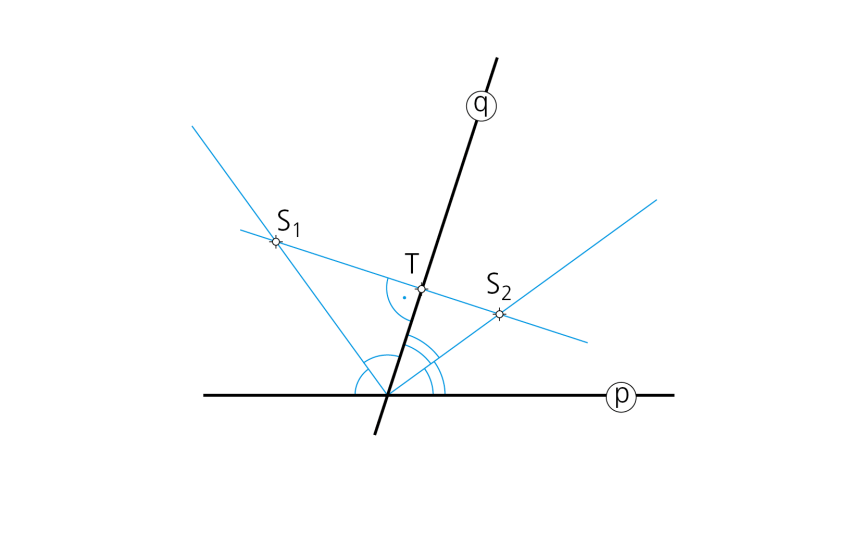
Paso 1- Se traza la perpendicular a la recta t por el punto T y se lleva el radio r en los dos sentidos, obteniendo así los puntos S1 y S2, centros de las dos posibles soluciones.
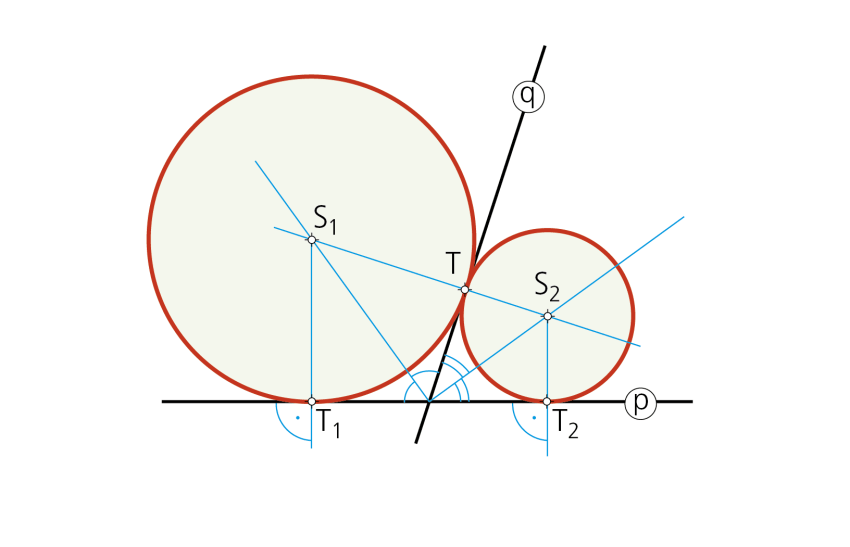
Paso 2- Como siempre, los puntos de tangencia T1 y T2 de cada solución con la recta p se obtienen trazando perpendiculares por los centros S1 y S2 de ambas soluciones.
A tres rectas que se corten entre sí.
Datos: Rectas a, b y c.
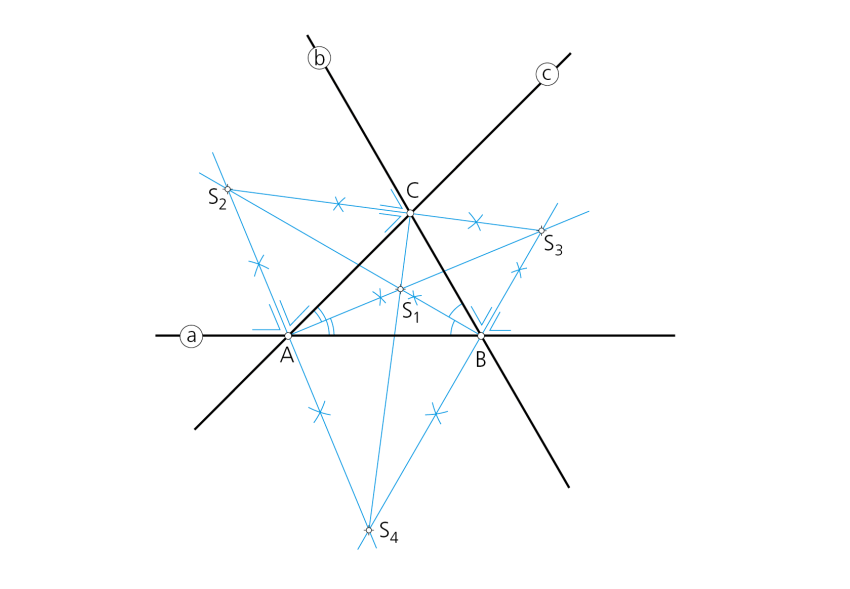
Paso1: Las rectas conforman el triángulo ABC, de vértices la intersección de las rectas dadas. El punto de corte de las bisectrices de los ángulos interiores del triángulo determinan el incentro (S1), centro de la circunferencia inscrita y primera de las soluciones. Análogamente, los puntos de corte de las bisectrices correspondientes a los ángulos exteriores definen los centros (S2, S3 y S4) de las otras tres circunferencias exteriores al triángulo ABC.
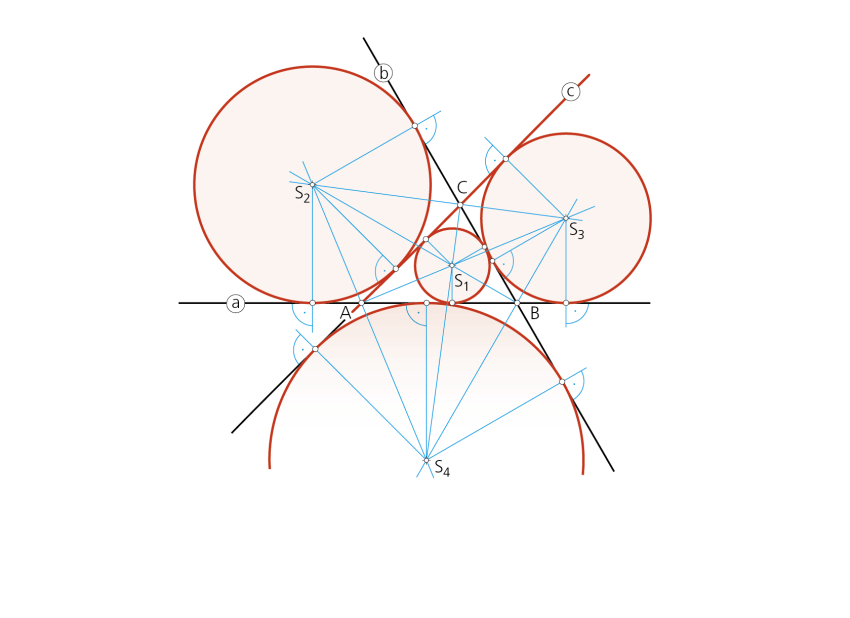
Paso 2- El radio de cada solución, como siempre, viene dado por la distancia del centro a cualquiera de las rectas. En la figura, se han señalado los puntos de tangencia de las soluciones con cada una de las rectas.
A una circunferencia de centro O en un punto T que ella y que pase por otro exterior P.
Datos: Circunferencia de centro O y puntos T y P.
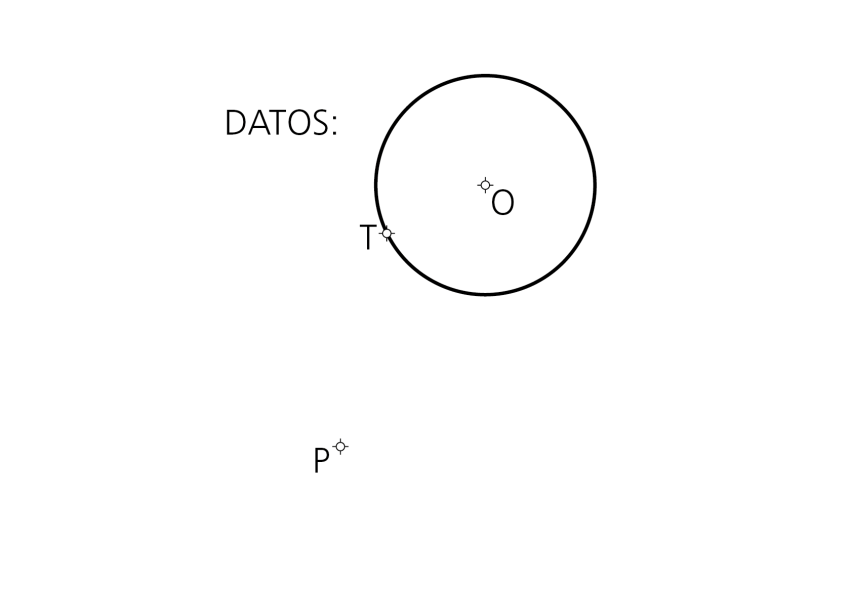
Datos: Circunferencia de centro O y puntos T y P.
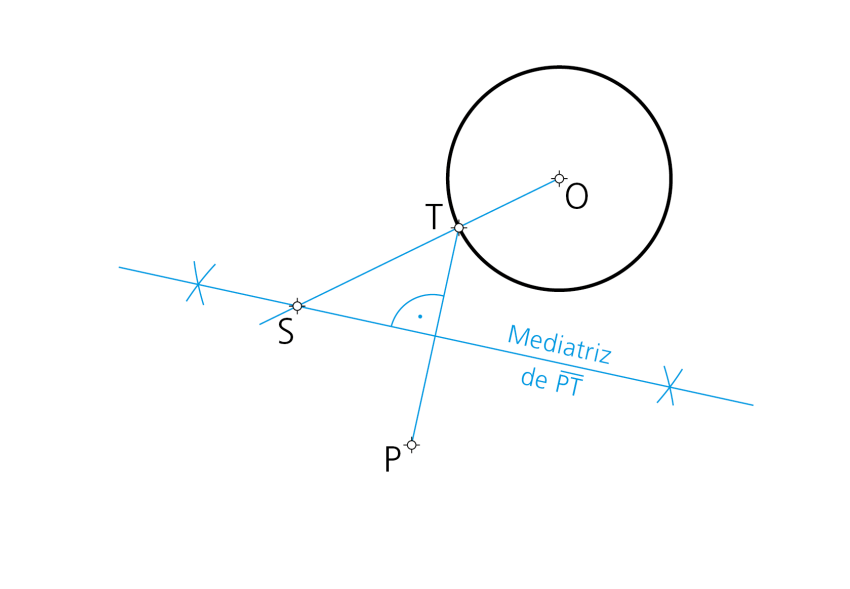
Paso 1- El problema queda resuelto al trazar la intersección de la recta OT (unión del centro de la circunferencia dada con el punto T de la tangencia) con la mediatriz del segmento PT , lo que determina el punto S centro de la circunferencia solución.
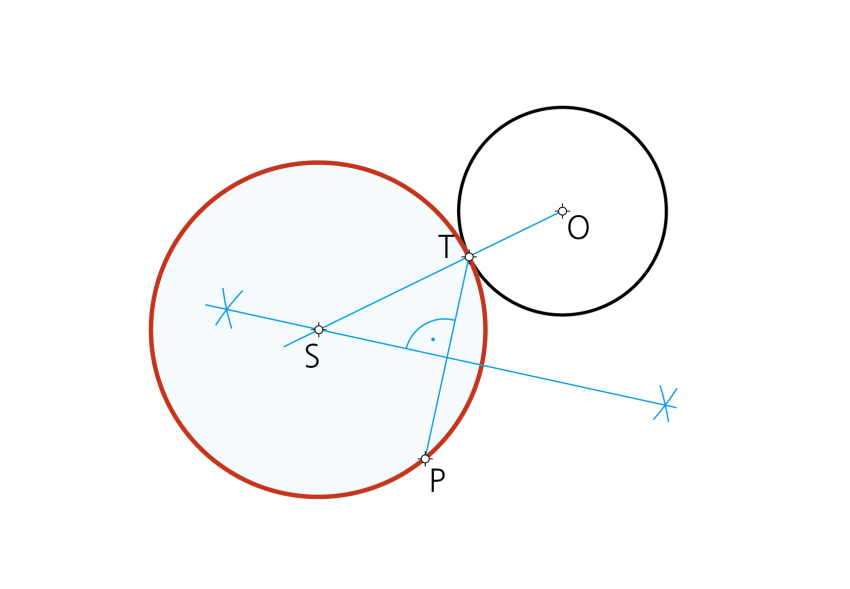
Paso 2- - Con centro en S y radio ST queda dibujada la única solución que es posible construir.
CURVAS EN LA ARQUITECTURA CLÁSICA
Es muy común en la arquitectura el uso de curvas, enlaces y tangencias como método constructivo para repartir las fuerzas de carga de una estructura o como método puramente decorativo para suavizar la dureza de la construcción.
Podemos encontrar arcos, elipses, ovoides, óvalos o espirales decorativas en multitud de periodos históricos y corrientes artísticas como, por ejemplo en el estilo clásico griego conocido como Jónico ( cuya columna identificativa se muestra en esta página) o en la obra de arquitectos de la talla del genio catalán Antonio Gaudí.
Como hemos dicho, la curva es un importante elemento estructural arquitectónico; el cual ayuda a sustentar el peso del edificio o distribuye la carga entre varios elementos.
El uso común de curvas en la arquitectura mediterránea europea ocurre a partir del medievo siendo frecuente utilizar arcos de medio punto y bóvedas de cañón. Con el tiempo evolucionó hacia nuevas ideas arquitectónicas que dieron lugar a bóvedas más complejas y esbeltas, nuevos elementos arquitectónicos y soluciones constructivas más inteligentes y eficaces. Un claro ejemplo se presenta en el uso extendido de contrafuertes exteriores a los muros de las catedrales góticas y renacentistas.
En ellos podemos ver perfectamente un arco de piedra que soporta y redirige el peso vertical del techo o de un muro hacia un pilar exterior ajeno a los propios muros de forma que soporta parte del peso sin interferir en la propia estructura. Esto facilitó crear muros más altos y estrechos, ventanas más grandes y estilizadas (lo que llevó a los grandes vitrales) y en general una nueva forma de entender la arquitectura a través del uso de enlaces y tangencias.
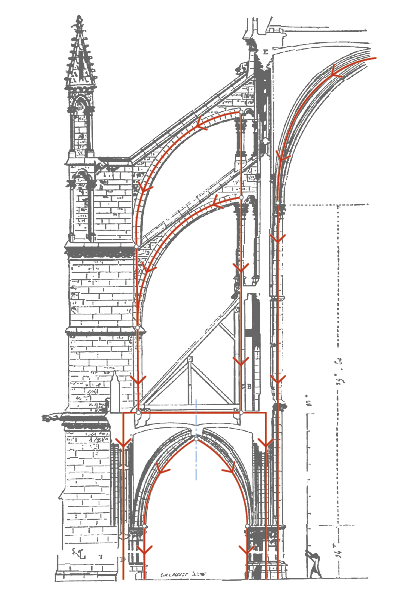
Ilustración del diccionario razonado de la arquitectura francesa de los siglos XI al XVI (1868).
Este dibujo, obra de Eugène Emmanuel Viollet le Duc permite mostrar la distribución de la carga de los muros hacia los contrafuertes exteriores y hacia el suelo de forma eficaz.

Arquitecto, conservador y restaurador de monumentos, nombrado superintendente de los edificios sagrados de Francia a mediados del siglo XIX. Fue responsable de la conservación y restauración de edificios medievales tan famosos como las catedrales de Notre-Dame y Amiens, de la basílica de Saint-Denis o del ilustre castillo medieval de Pierrefonds, entre otros. Realizó variados escritos y diseños en los que muestra una predilección por la arquitectura gótica y por recuperar su esencia aplicando, no obstante, nuevos materiales como el metal y el trabajo de forja en sus proyectos de arquitectura y decoración. Esto le generó controversia en su época siendo sus ideas aplicadas en corrientes estéticas más vanguardistas.
Eugène Emmanuel Viollet le Duc (1814-1879).

Columna Jónica.
El estilo Jónico griego se define como el epítome de lo estable, bello e intelectual con un buen equilibrio entre estética y funcionalidad..