2- TRIÁNGULOS
TANGENCIAS Y CURVAS TÉCNICAS
Enlaces
Unidad 4
2• ENLACES
Se llama enlace o empalme, en los trazados geométricos, a la unión de rectas con curvas o de curvas entre sí, efectuadas por medio de su punto de tangencia. Este punto común es el que permite la transición suave de unas a otras sin brusquedades de ningún tipo.
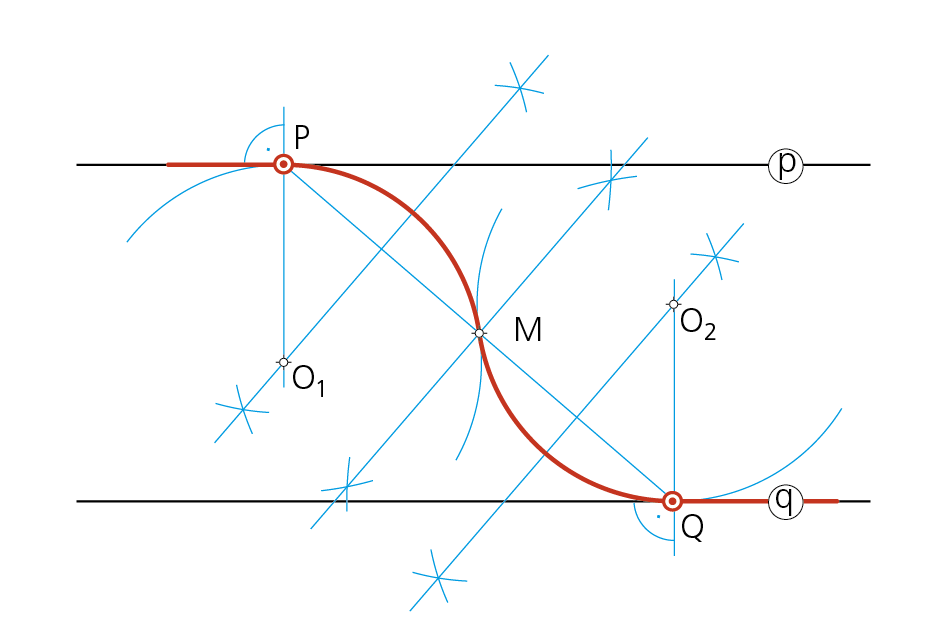
2.1 Enlazar dos rectas paralelas p y q mediante dos arcos iguales, conociendo los puntos de tangencia P y Q sobre ellas.
• Paso 1 - Al ser los arcos iguales, el enlace se producirá en el punto medio M del segmento PQ.
• Paso 2 - Los centros de los arcos se encontrarán en la intersección de las perpendiculares a las rectas p y q por los puntos de tangencia P y Q, con las mediatrices de los segmentos PM y MQ respectivamente.
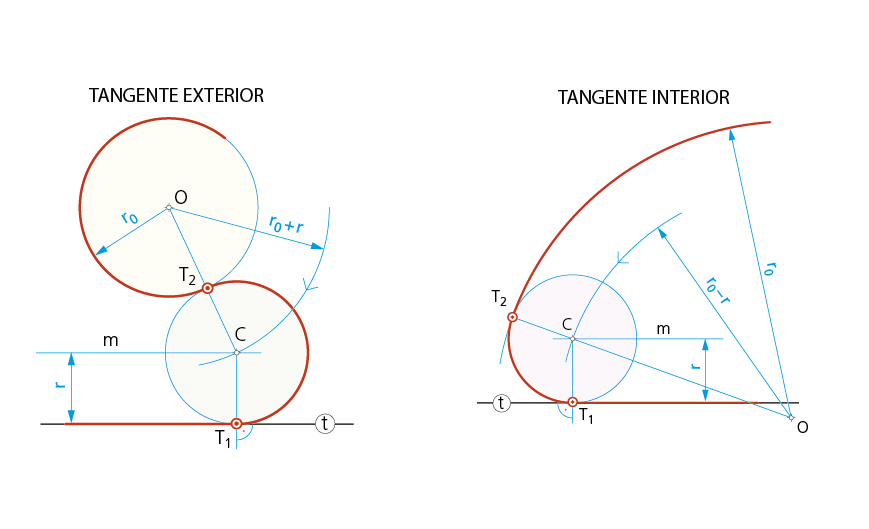
2.2. Enlazar una recta t y un arco de circunferencia de centro O y radio r0 por medio de un arco de circunferencia de radio r.
•Pueden darse dos casos: bien que la circunferencia solución sea tangente exterior o bien que sea interior a la circunferencia dada. En ambos casos se trazan la recta m, paralela a t, distante r, y las circunferencias de radio (r0 + r) o (r0 - r), respectivamente, que determinan el punto de intersección C, centro del arco de enlace en ambos casos.
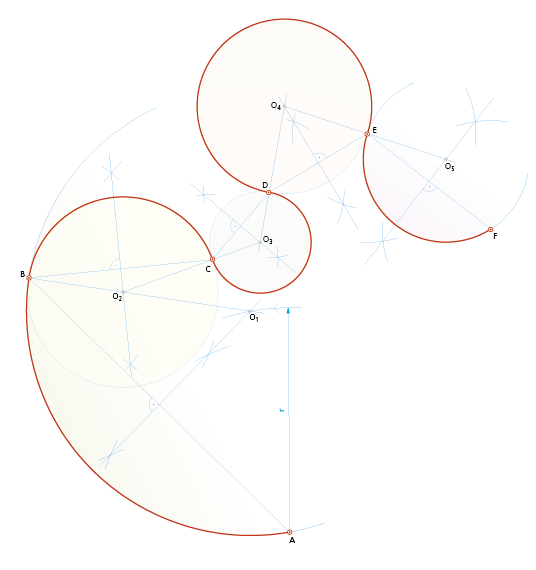
2.3. Enlazar varios puntos A, B, C,... no alineados, mediante arcos de circunferencia, conociendo el radio r de uno de los arcos.
Se trata de ir uniendo los puntos de una poligonal (A-B-C-D-E-F), con arcos de circunferencia tangentes entre sí.
Para ello, se ha de tener en cuenta que los centros de las circunferencias están en la mediatriz de cada segmento, y también que, para que la curva sea tangente a la anterior, ha de estar en la recta que une los centros de ambas.
El punto de intersección de las rectas –mediatriz y línea de centros –determina el centro del arco de circunferencia que pasa por los dos puntos considerados.
• Paso 1 - Se comienza trazando la mediatriz del segmento AB y, con centro en A y radio r (dado), se traza un arco que corta a la mediatriz en el punto O1, centro del arco que pasa por dichos puntos.
• Paso 2 - Se unen los puntos B y C, trazando la mediatriz del segmento que corta a la recta O1B en el punto O2. Con este centro se traza el arco BC, que es tangente al anterior en B.
• Paso 3 - Se unen los puntos C y D trazando la mediatriz del segmento, que corta a la recta O2C en el punto O3. Con centro en O3 se traza el arco CD, tangente al anterior en C y así sucesivamente.