TANGENCIAS Y CURVAS TÉCNICAS
ÓVALOS, OVOIDES Y ESPIRALES
Unidad 4
3• TRAZADO DE CURVAS TÉCNICAS: ÓVALOS, OVOIDES Y ESPIRALES
Los óvalos y ovoides pertenecen al grupo de los enlaces denominados cerrados dado que comienzan y terminan en un mismo punto. También son denominadas curvas circulares cerradas debido al hecho de estar formadas por circunferencias tangentes entre sí.
3.1 Óvalo
Se denomina óvalo a la curva cerrada y convexa, con dos ejes de simetría perpendiculares, compuesta por un número par de arcos de circunferencia tangentes entre sí, cuyos centros se hallan en los ejes de simetría.
3.1.1. Óvalo dado el eje mayor: óvalo de tres partes.
Sea AB la magnitud del eje mayor del óvalo.
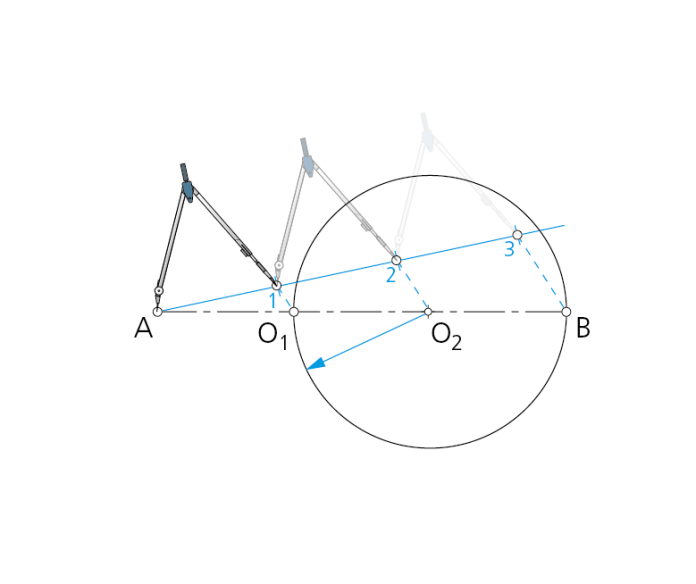
Paso 1 - Se divide el segmento AB en tres partes iguales, obteniendo los puntos O1 y O2.
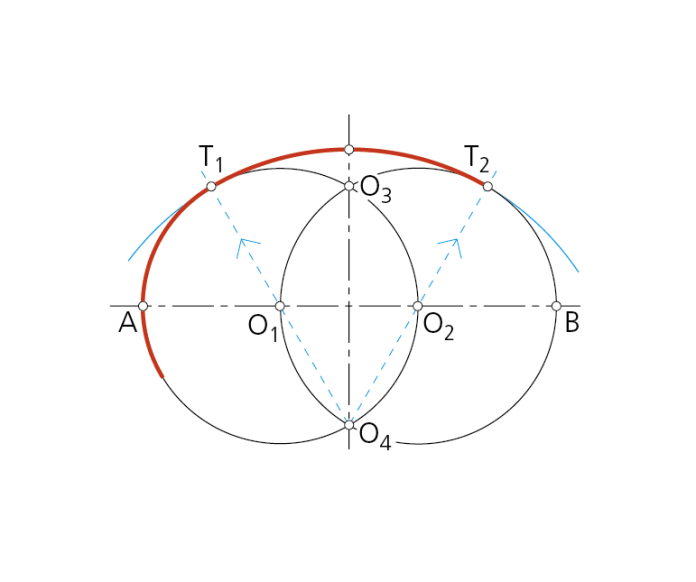
Paso 2 - Con centro en O1 y O2 se trazan las circunferencias de radios iguales a la tercera parte del diámetro AB.
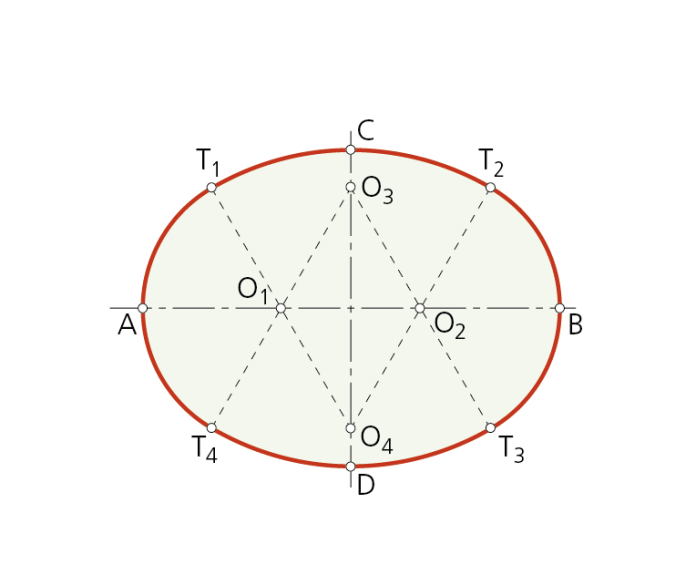
Paso 3 - Los puntos O3 y O4, comunes a ambas circunferencias, determinan los centros de los otros dos arcos tangentes a las circunferencias primitivas en los puntos T1, T2, T3 y T4.
3.1.2. Óvalo dado el eje mayor: óvalo de cuatro partes.
Sea AB el eje mayor dado.
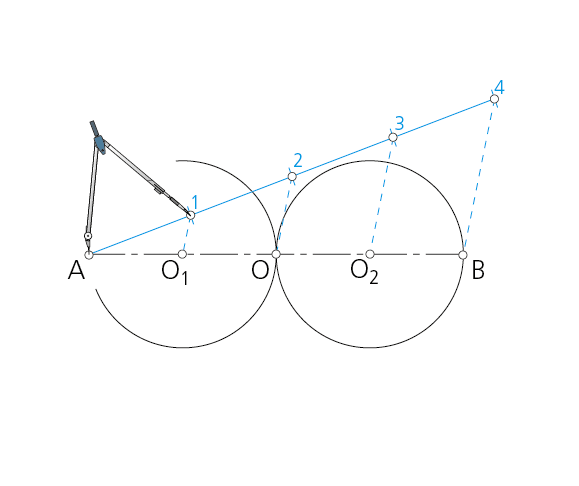
Paso 1 - Se divide el segmento AB en cuatro partes iguales, obteniéndose los puntos O1, O y O2.
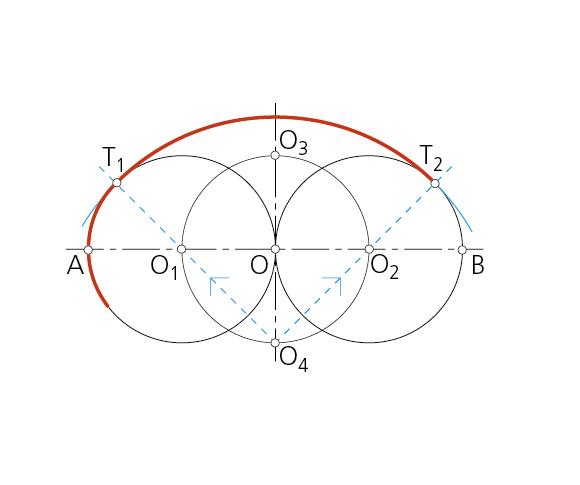
Paso 2 - Con centro en O1, O y O2 se trazan las circunferencias de radios iguales a AB/4
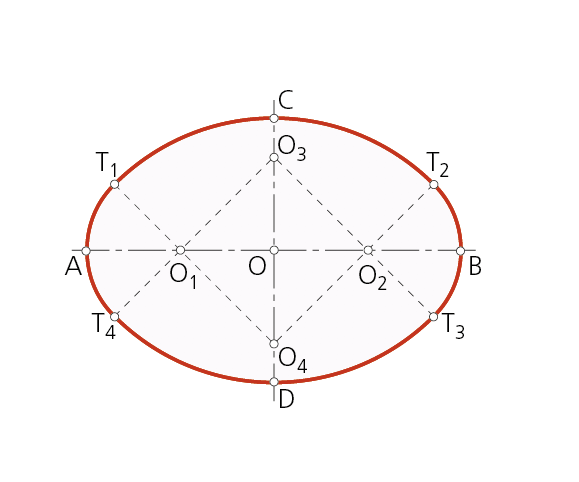
Paso 3 - La circunferencia de centro O cortará a la mediatriz de AB (eje menor del óvalo) en los puntos O3 y O4, centros de la otra pareja de circunferencias tangentes a las primitivas en los puntos T1, T2, T3 y T4, obtenidos uniendo los centros de los arcos tangentes correspondientes.
3.1.3. Óvalo conocido el eje menor.
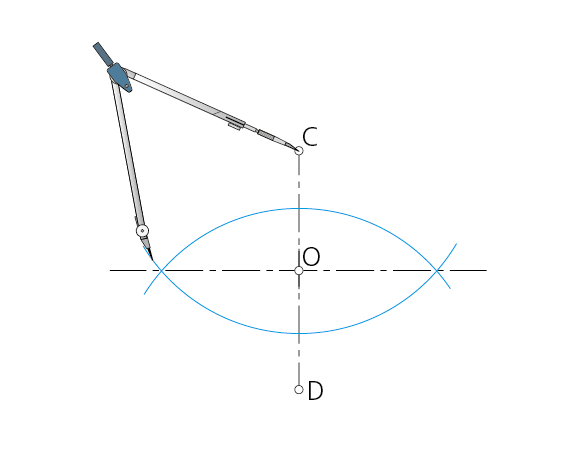
Paso 1 -Sea CD el eje menor del óvalo. Se traza la mediatriz del segmento CD, obteniendo el punto medio O, centro de la circunferencia de radio CD/2.
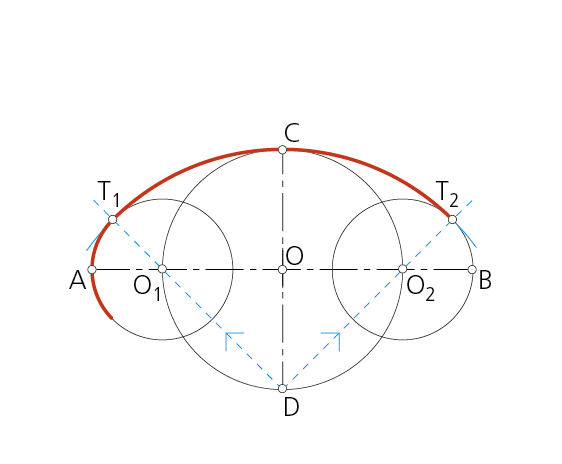
Paso 2 - Los puntos O1 y O2, intersecciones de la mediatriz anterior con la circunferencia dibujada, resultan ser los centros de los arcos menores del óvalo. Los extremos C y D del eje menor son los centros de los arcos mayores.
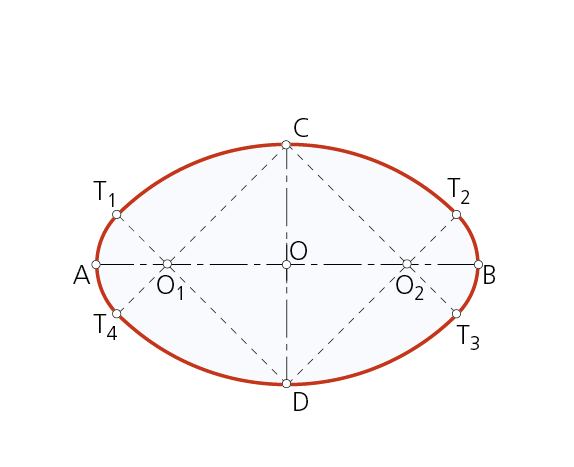
Paso 3 - La unión de C y D con O1 y O2 determina los puntos de enlace T1, T2, T3 y T4 de los cuatro arcos de circunferencia.
3.1.4. Óvalo conocidos los dos ejes.
Sean AB y CD las magnitudes de los ejes considerados.
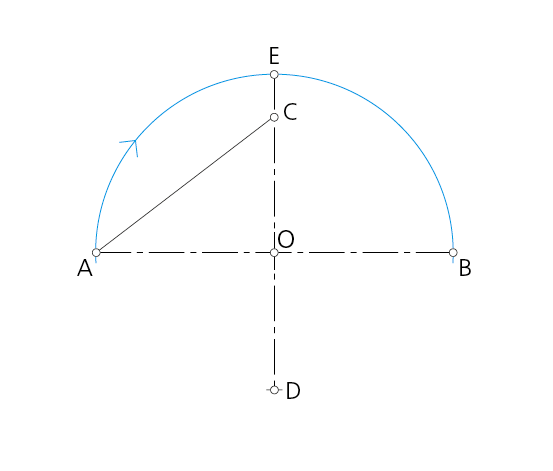
Paso 1 -- Se dibujan los ejes AB y CD perpendiculares entre sí, cortándose en su punto medio O. Con centro en O y radio el semieje mayor se traza un arco hasta cortar a la prolongación del eje menor en el punto E.
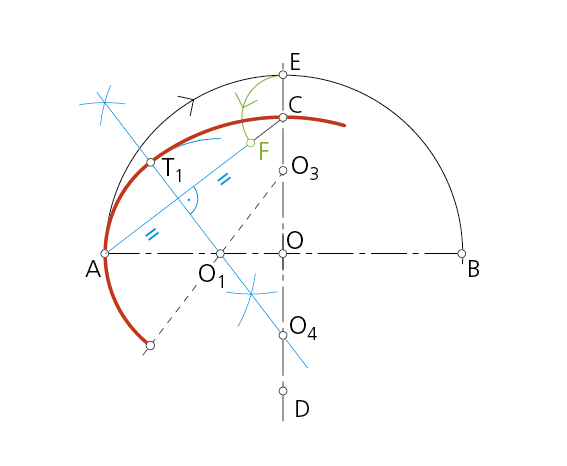
Paso 2 - Con centro en C y radio CE se traza otro arco que corta al segmento AC en F. A continuación se traza la mediatriz del segmento AF, que corta a los ejes dados en O1 y O4.
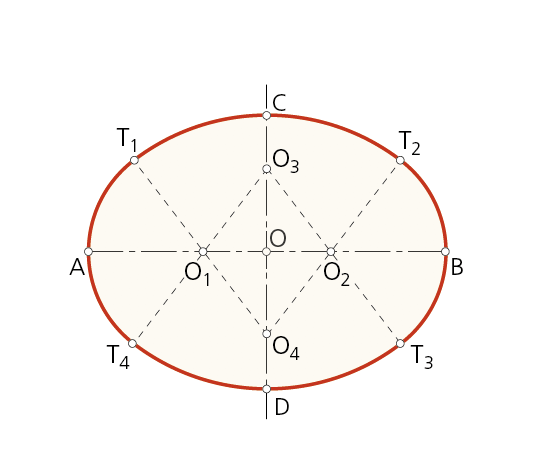
Paso 3 - Los puntos O1 y O4, junto con los puntos O2 y O3, simétricos de los anteriores respecto al centro O de la curva, son los centros de los cuatro arcos que forman el óvalo.
3.1.5. Óvalo inscrito en un rombo
Óvalo isométrico. • Cuando el óvalo se encuentra inscrito en un rombo de ángulos 120° y 30°, toma el nombre de óvalo isométrico, denominado así por corresponder, convencionalmente, a las circunferencias representadas en el Sistema Isométrico de representación cuando éstas son paralelas a los planos coordenados del sistema tridimensional.
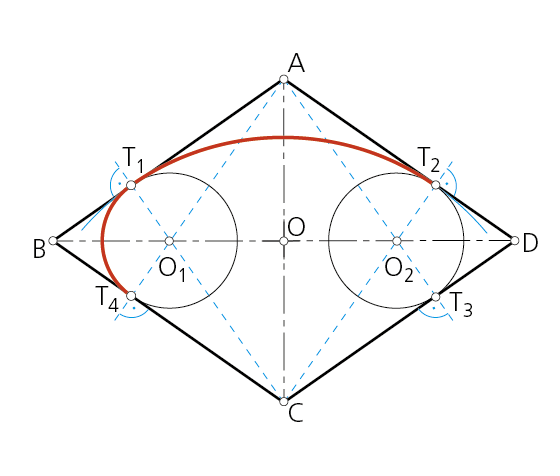
Paso 1 - Sea el rombo ABCD, cuyas diagonales se cortan en su punto medio O. Desde los vértices obtusos del paralelogramo, puntos A y C, se trazan perpendiculares a los lados opuestos, determinando los puntos O1 y O2, centros de los arcos menores del óvalo.
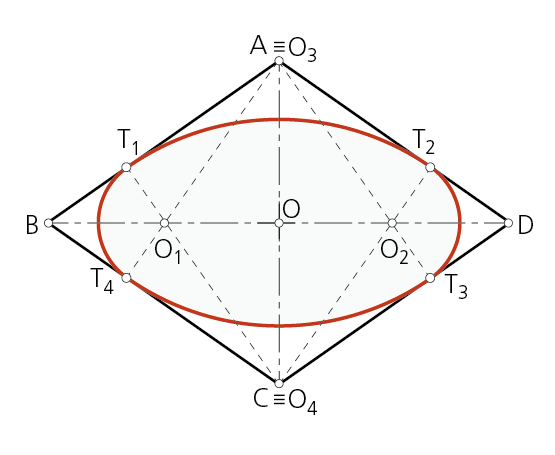
Paso 2 - Los puntos A y C son los centros O3 y O4 de los arcos mayores que completan y cierran el óvalo.
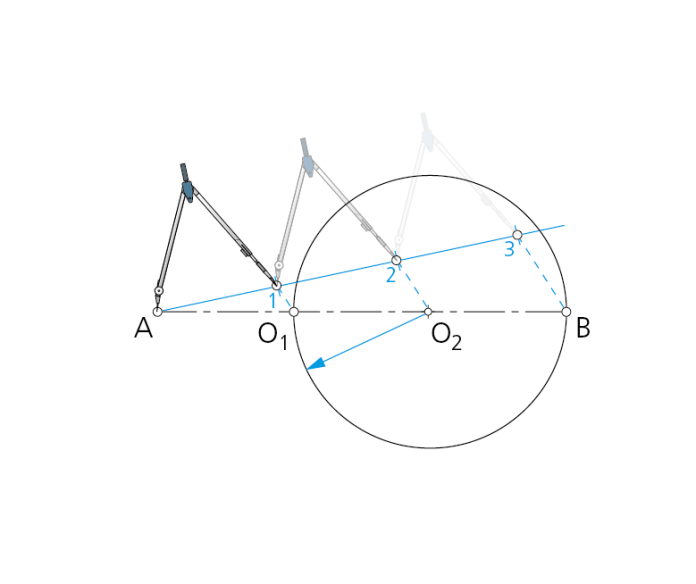
Paso 1 - Se divide el segmento AB en tres partes iguales, obteniendo los puntos O1 y O2.

Paso 2 - Con centro en O1 y O2 se trazan las circunferencias de radios iguales a la tercera parte del diámetro AB.

Paso 3 - Los puntos O3 y O4, comunes a ambas circunferencias, determinan los centros de los otros dos arcos tangentes a las circunferencias primitivas en los puntos T1, T2, T3 y T4.
3.2 Ovoide
Se denomina ovoide a la curva cerrada y convexa, formada por arcos de circunferencia tangentes entre sí, dependientes de un único eje de simetría. Se trata de una curva muy parecida al contorno de un huevo (de ahí su denominación) y su trazado es eminentemente empírico, lo que trae consigo la existencia de un gran número de construcciones. Aquí analizamos alguno de los trazados más utilizados.
3.2.1 Ovoide conocido el eje no simétrico.
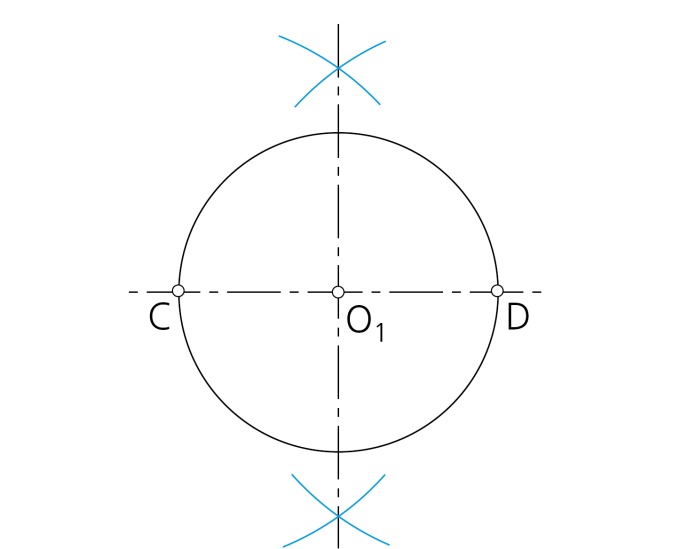
Paso 1 -Dado el diámetro CD del ovoide, se traza su mediatriz para determinar su punto medio O1 y se dibuja la circunferencia de centro este punto y radio CD/2.
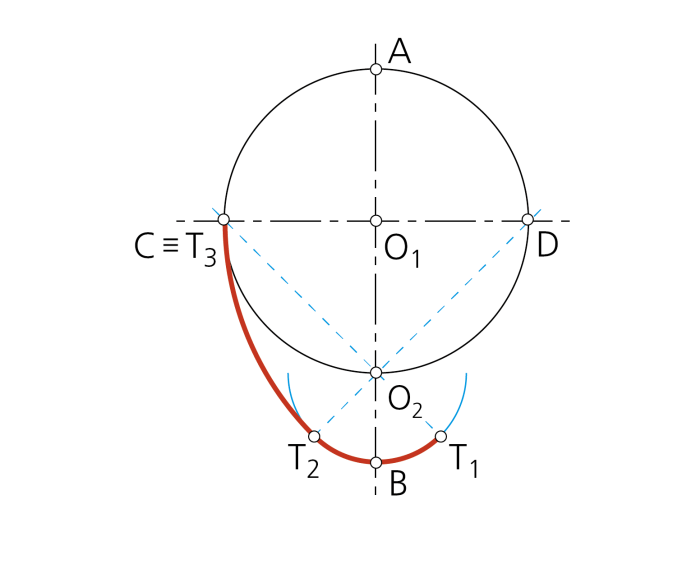
Paso 2 - La mediatriz antes trazada, eje de simetría del ovoide, corta a la circunferencia dibujada en el punto O2 centro del arco menor de la curva. La unión de este punto con C y D determina los puntos de enlace T1 y T2.
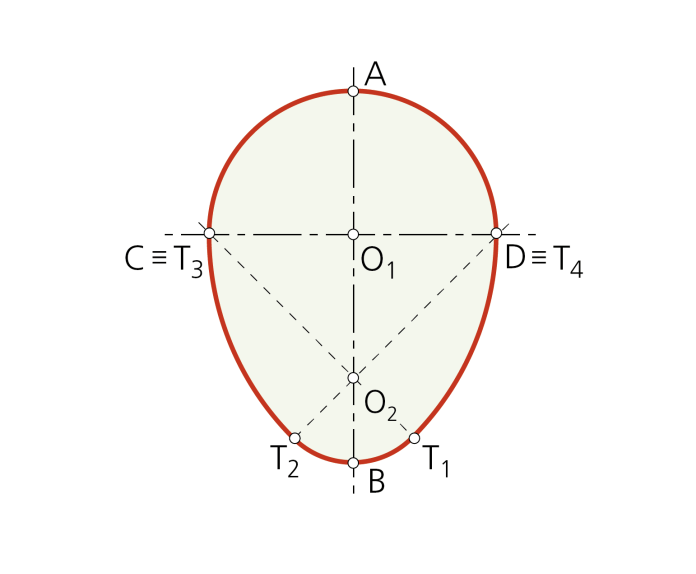
Paso 3 - Con centro en C y D se trazan los arcos mayores que además corresponden con los puntos de enlace T3 y T4 respectivamente. Se completa el ovoide con la semicircunferencia de centro O1 y radio O1A.
3.2.2. Ovoide común a dos circunferencias de centros y radios dados.
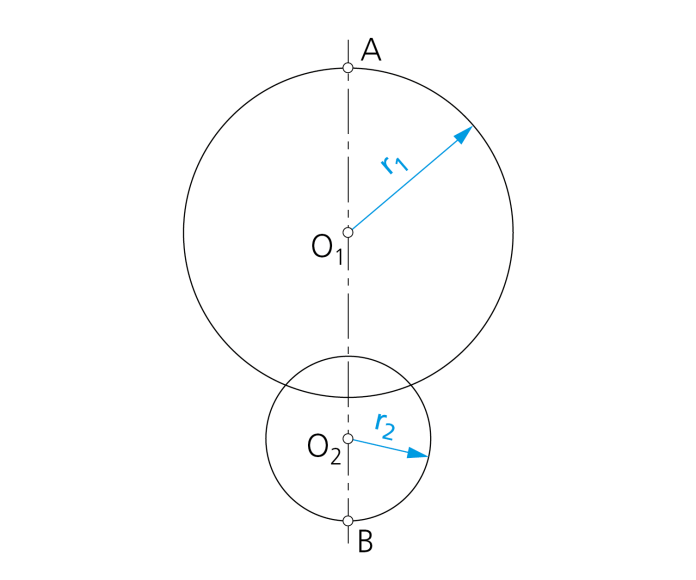
Paso 1 - Se parte de conocer los centros O1, O2 y radios respectivos de dos circunferencias secantes cuyo diámetro común es el eje de simetría del ovoide.
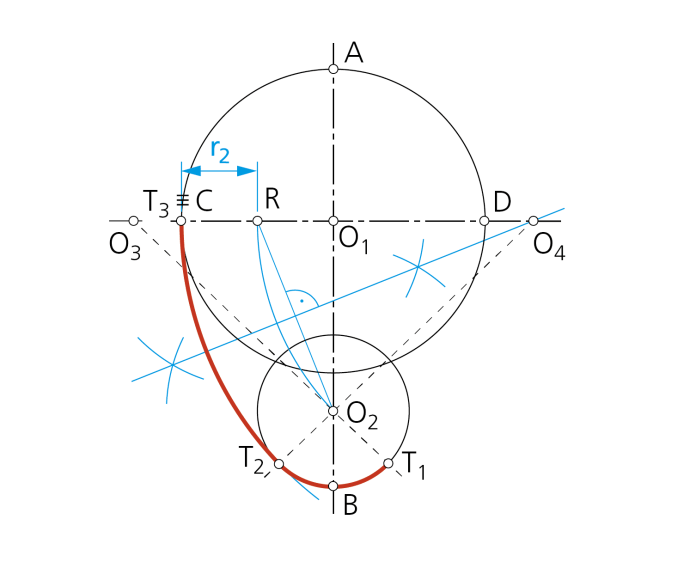
Paso 2 - El trazado se simplifica al considerar que el arco solución de centro O3 o O4 es concéntrico al que pasa por el punto O2 y por un punto R del diámetro CD, tal que CR = r2; basta con trazar la mediatriz de O2R para hallar O4 y consiguientemente O3, simétrico de él, respecto del eje.
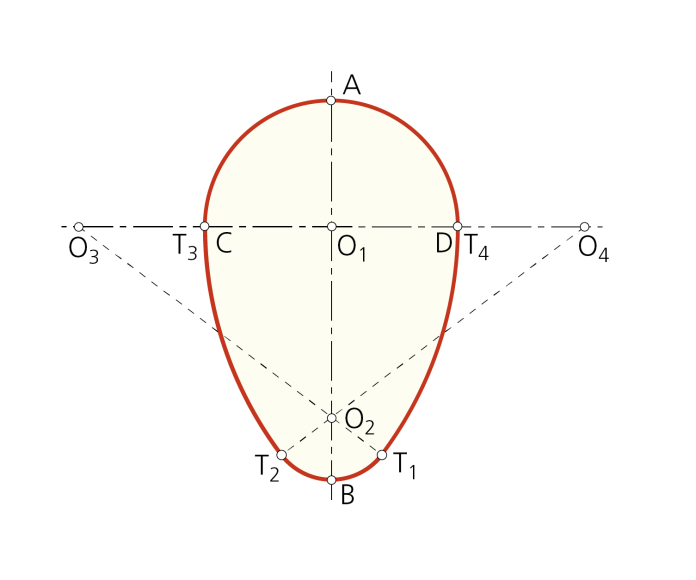
Paso 3 - Localizados los cuatro centros O1, O2, O3 y O4 que determinan el ovoide y definidos los puntos de enlace T1, T2, T3 y T4 el trazado completo de la curva es inmediato.
3.3 Espirales Propiedades fundamentales
Las espirales son curvas abiertas y planas, generadas por el movimiento de un punto que se desplaza gradualmente alrededor de otro fijo, alejándose de él en cada vuelta. La distancia radial que existe entre dos vueltas o espiras consecutivas se denomina «paso» de la espiral.
3.3.1 Espiral de base un segmento AB.
Está formada por arcos semicirculares tangentes entre sí, con centros en los extremos del segmento AB dado. Los puntos de tangencia se encuentran sobre la recta determinada por los centros y el paso de la espiral es igual al doble de la distancia entre centros.
Las espirales crecen progresivamente de forma que si el segmento original mide 6 mm, el primer radio mide 12mm, el segundo 18mm...
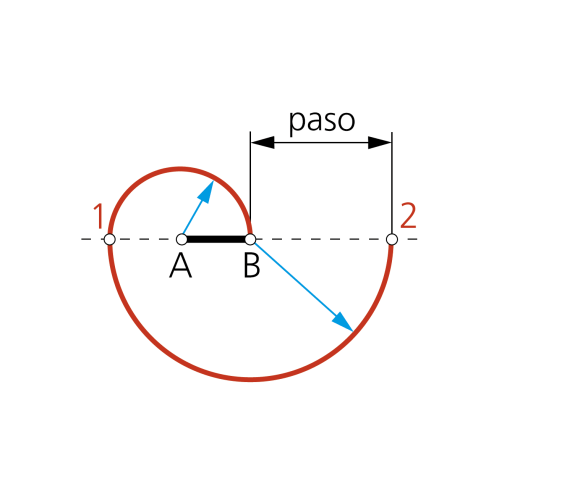
Paso 1 -Con centro en A y en B, extremos del segmento dado, considerado como núcleo de la espiral, se van trazando arcos de radio variable e iguales a las distancias respectivas de A y de B a los puntos que van obteniéndose.
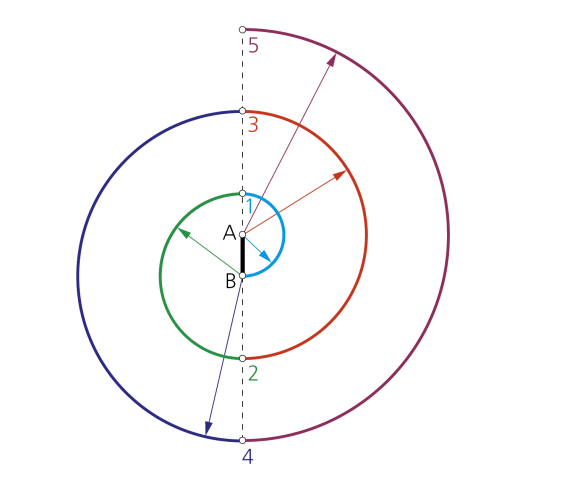
Paso 2 -
Obsérvese cómo los radios van creciendo sucesivamente en AB, siendo el paso de esta espiral el doble de la longitud del segmento base, esto es: p = 2 • AB.

Trazado si el vértice no está localizado.
Nautilus. Sección sagital de la concha externo de un molusco de la familia de los cefalópodos que presenta una espiral logarítmica casi perfecta




3.2.2. Espiral de núcleo poligonal o volutas de varios centros.
En este tipo de espirales los centros de los arcos-enlaces se consideran situados en los vértices de un módulo base formado por los vértices de polígonos, regulares o irregulares.
Los radios se forman prolongando ordenadamente los lados del polígono y sumando sucesivamente el siguiente con el anterior, hasta completar una vuelta, que ocurrirá cuando la curva voluta haya empleado todos los vértices del polígono.
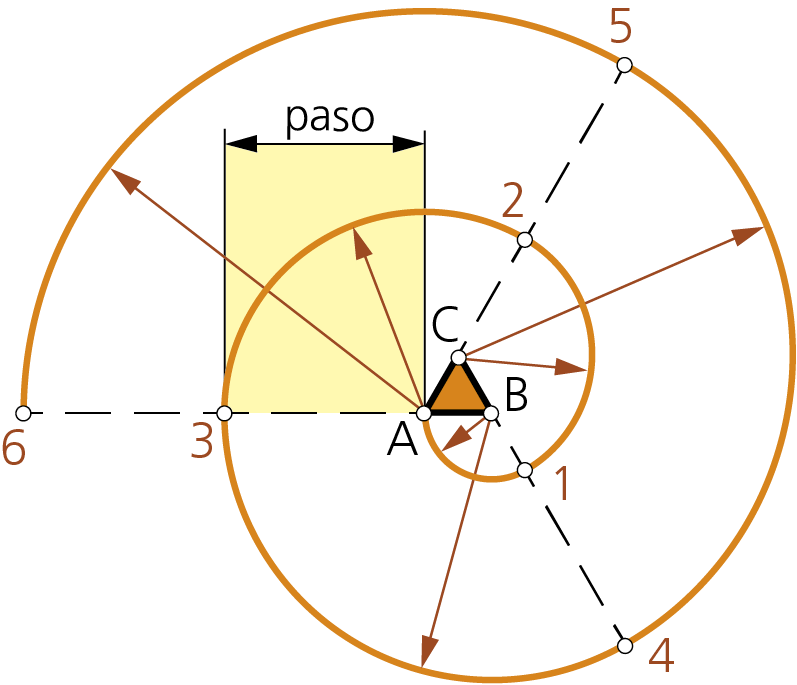
• Voluta de tres centros.
Se trata de una espiral de base un triángulo equilátero ABC prolongando sus lados y de lado la tercera parte del paso (p/3). El «paso p» de la espiral (voluta) será igual al perímetro del triángulo; es decir, tres veces el lado.
Para su trazado, se hace centro en uno de los tres vértices y se van trazando arcos de circunferencia de radios crecientes sucesivamente en p/3.
Así, con centro en B se lleva el radio BA = p/3; con centro en C el radio C1 = 2 • p/3; con centro en A el radio A2= 3 • p/3=p, lo que completa una vuelta y determina la magnitud del paso de la curva. Así sucesivamente, siempre con amplitud del ángulo 120°.
• Voluta de cuatro centros.
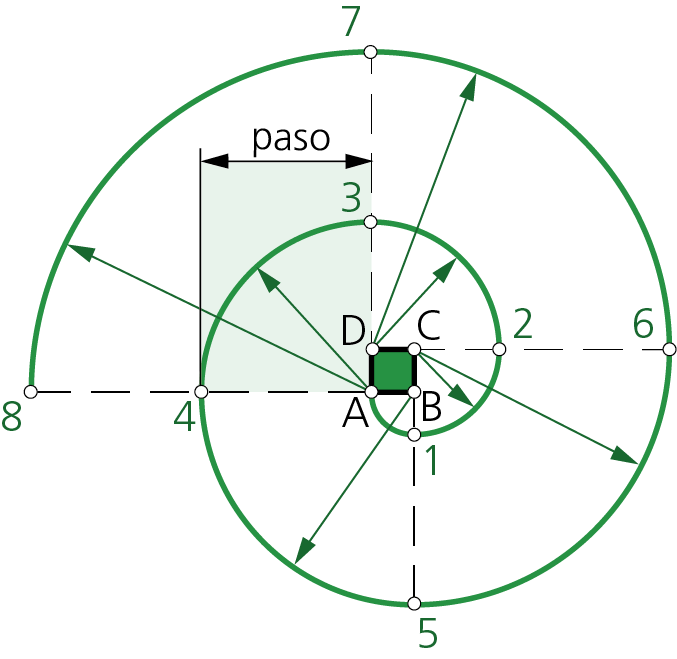
Como en el caso anterior, los centros se encuentran en los vértices, siendo sus radios: p/4, 2 • p/4, 3 • p/4, 4 • p/4, etc. y la amplitud del ángulo 90°. El «paso p» de la espiral es igual al perímetro del cuadrado base que genera la voluta. Un nuevo recorrido, con arcos centrados en los vértices, crea tantas espirales como vueltas se describan.
En la figura, la curva nace en el vértice A del cuadrado, con un arco de centro B y radio el lado del polígono.Siguiendo con el arco de centro C y radio 2 • p/4 enlaza otro cuarto de circunferencia que va del punto 1 al 2, y así, sucesivamente, hasta alcanzar la primera vuelta en el punto 4.
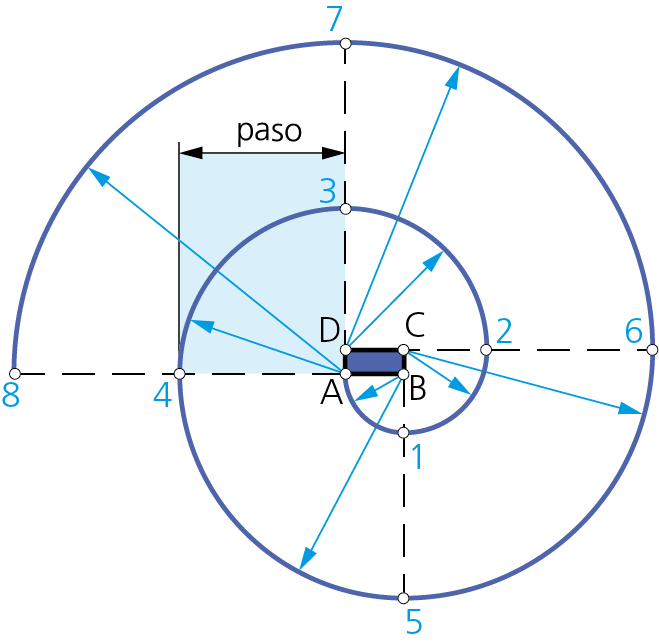
• Espiral de base un rectángulo.
Cuando el módulo base es un polígono irregular, como en este caso, la espiral cambia rápidamente su trayectoria, alternando, de modo también brusco, aunque parcialmente constante, las longitudes de sus radios.
Como en los casos anteriores, el «paso p» de la voluta es igual al perímetro del rectángulo base.
A partir del rectángulo base ABCD, el primer cuadrante de arco, de centro B, va del vértice A al punto 1 de enlace con el siguiente, siendo su radio el lado mayor del polígono base.
Los puntos de enlace situados en las prolongaciones de los lados menores del rectángulo centran las trayectorias de menor curvatura, mientras que los de mayor curvatura se encuentran en las prolongaciones de los lados mayores.
ESPIRAL ÁUREA
Formada por arcos de circunferencia tangentes entre sí, verificándose que la razón de radios consecutivos es constante e igual al número de oro φ.
El trazado, como se aprecia, nace en sentido contrario a lo establecido normalmente, esto es, de fuera a dentro hasta los límites naturales en que la trayectoria pueda ser secuenciada visualmente.
Así, se cumple que: r1/r2 = r2/r3 = ... = φ = 1,618033989...
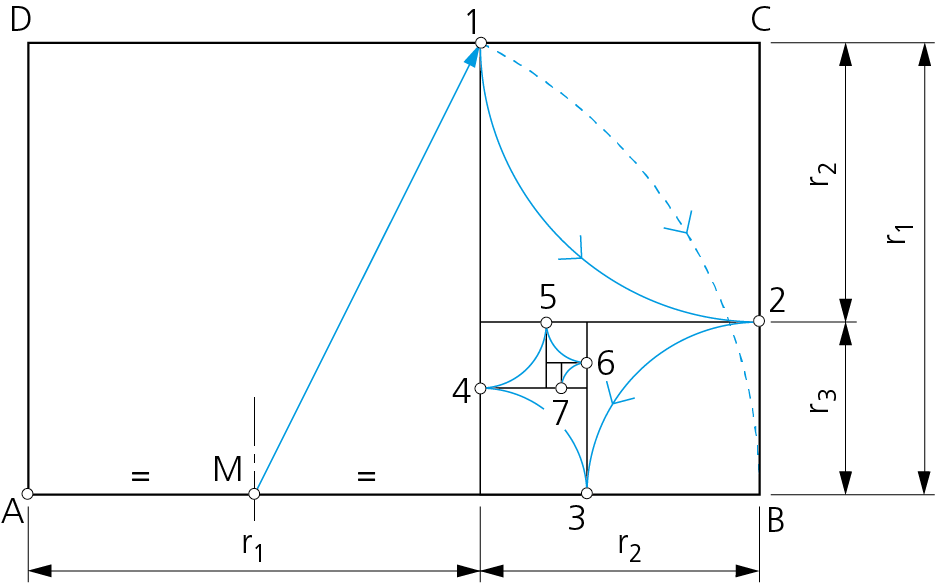
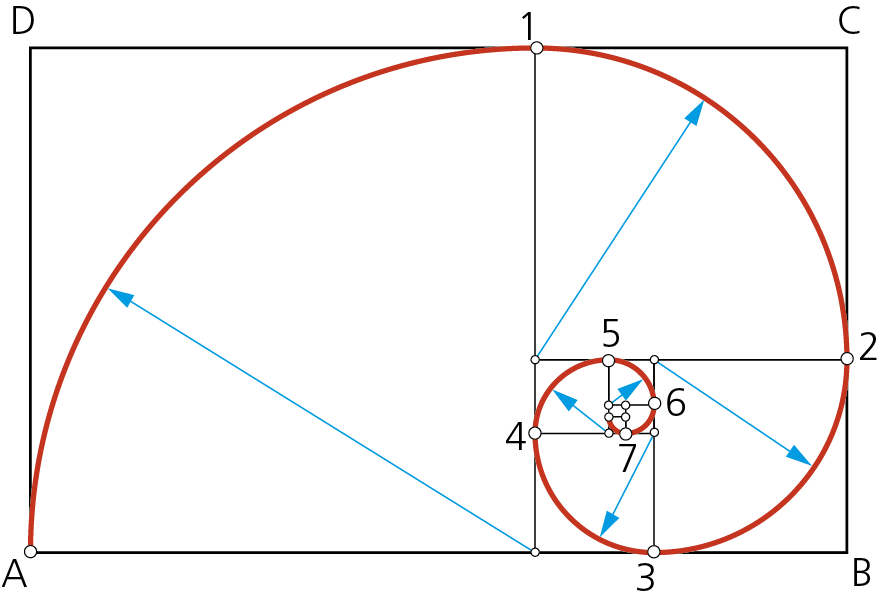
Se comienza por dibujar un rectángulo áureo ABCD de relación entre lados el valor φ. A partir de él se determina, como se aprecia en la figura, la serie correspondiente de subrectángulos áureos.
A continuación se trazan los arcos de circunferencia inscritos en los cuadrados. La sucesión ordenada de los mismos determina la espiral áurea.
ESPIRAL LOGARÍTMICA
Es la más relevante de todas las espirales, también denominada espiral mística o natural por su frecuente presencia en la naturaleza.
La espiral logarítmica es la curva que responde a la expresión exponencial en coordenadas polares: r = k·eω siendo r el radio vector, k una cte. y ω el argumento.
En el procedimiento de trazado que se expone, suponemos dos rectas perpendiculares, a modo de ejes, que se cortan en el punto-origen O.
Se traza un triángulo rectángulo de catetos OA y OB donde OA = r (medido según una unidad arbitraria, u = 1) y OB = 1. La curva, por tanto, será de mayor alargamiento o achatamiento, dependiendo de la relación OA / OB entre los catetos.
Definido el triángulo rectángulo AOB, por el vértice B se traza una perpendicular a la hipotenusa, obteniendo sobre el otro eje el punto C, por el que, a su vez, se trazará otra perpendicular al segmento BC, obteniendo el punto D sobre el otro eje y así sucesivamente.
Es de observar que la espiral no llegará a alcanzar jamás el origen O, si bien se aproximará a él infinitamente.
La curva, obviamente, se traza a mano alzada como puede verse en la espiral de color verde a la derecha de estas líneas. No obstante dado que, gráficamente, se ajusta bastante al enlace de arcos de circunferencia, es posible determinar sus centros OAB, OBC, OCD,… como intersección de las mediatrices de los segmentos AB, BC, CD,… con las bisectrices de los ángulos rectos correspondientes. Este trazado puede observarse en el último dibujo de este cuadro.
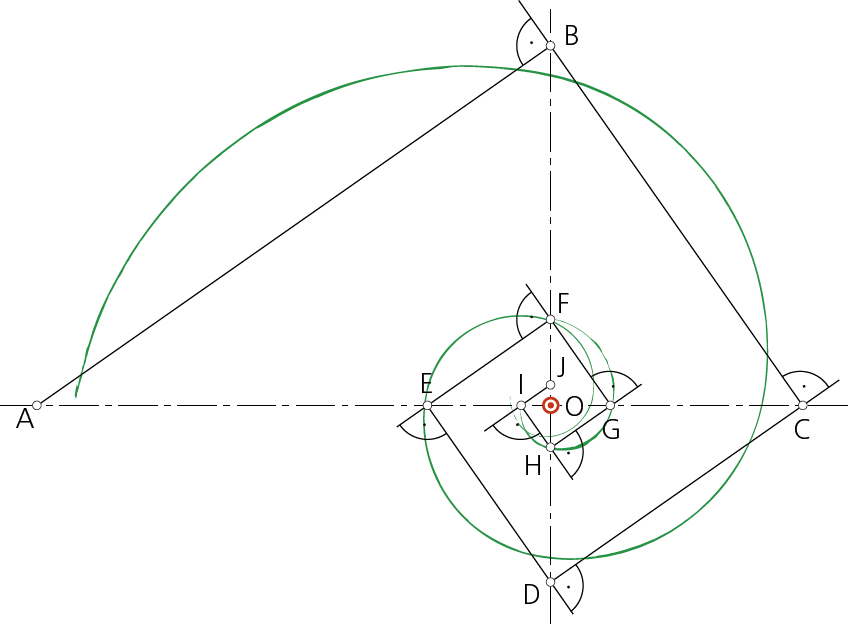
Espiral con trazado a mano alzada.
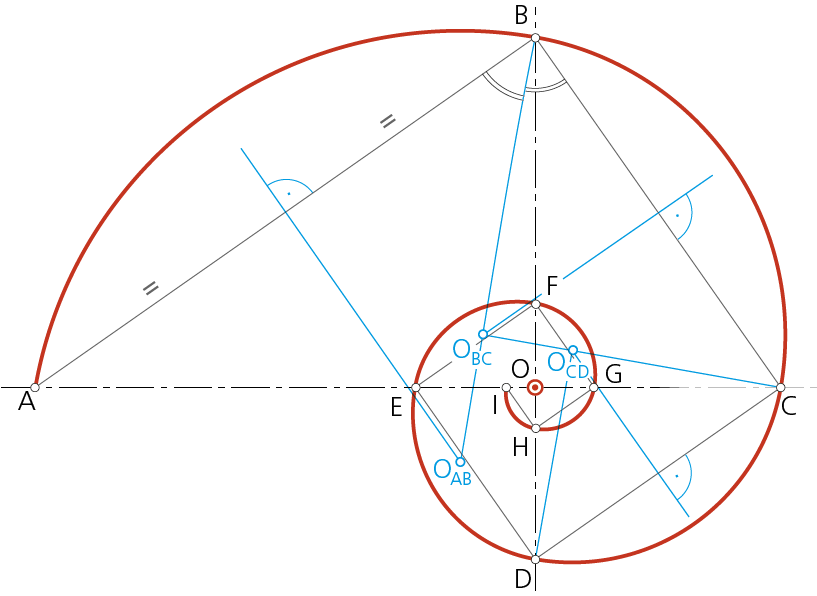
Espiral con trazado geométrico aproximado.