SISTEMA DIÉDRICO
Síntesis del Sistema diédrico
Unidad 6
2• REPRESENTACIÓN DEL PUNTO
2.1. Represeentación
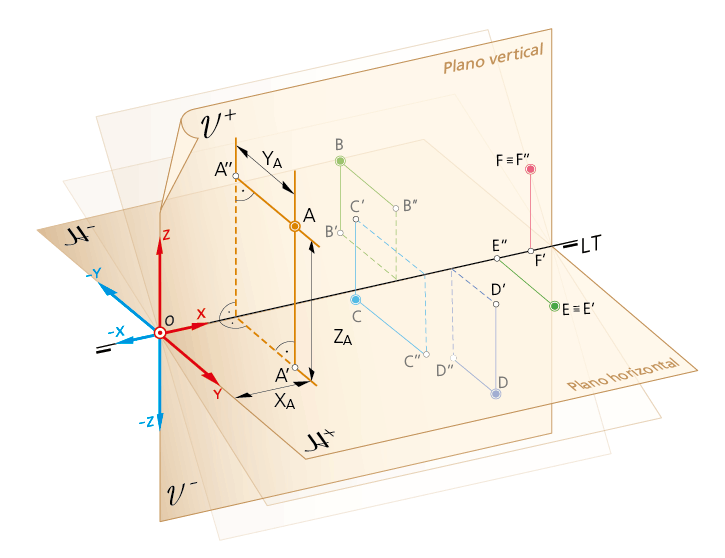
Si imaginamos un punto A en el espacio la proyección ortogonal sobre el plano horizontal H es un punto A’ y sobre el plano vertical V otro punto A’’. Estas dos proyecciones A’ y A’’ representan el punto A en el espacio. Esta representación es reversible, esto es, si se conocen las proyecciones A’ y A’’, el punto A estaría en la intersección de las perpendiculares a H y V, por A’ y A’’, respectivamente.
Todo punto del espacio se ubica mediante sus tres coordenadas cartesianas referidas al triedro de ejes con origen en un punto (O) de la LT, siendo:
• XA: la coordenada desplazamiento. Con referencia a un plano de perfil que pasa por el origen de coordenadas.
• YA: la coordenada alejamiento. Distancia del punto A al plano vertical (AA’’). Alejamientos positivos son los que ocupan aquellos puntos situados por delante del plano vertical V.
• ZA: la coordenada cota o altura. Distancia del punto A al plano horizontal (AA’ ). Se considera positiva, cuando el punto está situado por encima del plano horizontal H .
2.2 Posición en el espacio
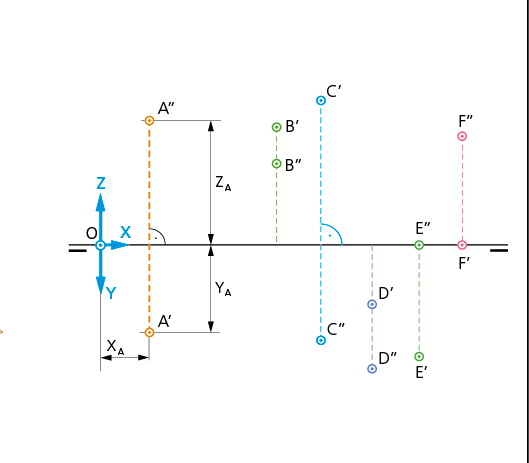
Las infinitas posiciones que un punto puede tener en el espacio respecto a los planos de proyección siguen unas pautas generales: todos los puntos situados en el cuadrante I y II tienen su proyección vertical por encima de la LT (cota positiva) y los del cuadrante III y IV por debajo de la LT (cota negativa). Asimismo, los puntos del cuadrante I y IV tienen su proyección horizontal por delante de la LT (alejamiento positivo) y los del II y III por detrás de la LT (alejamiento negativo).
El punto A (alejamiento y cota +) ejemplifica la posición de todos los puntos ubicados en el I cuadrante. Su proyección horizontal A’ está por debajo de la LT y la proyección vertical A’’ por encima de ésta.
El punto B en el II cuadrante (cota + y alejamiento -) hace que la representación diédrica de B’ y B’’ se presenten ambas por encima de la LT.
El punto C en el III cuadrante (cota y alejamiento -) tiene su proyección C’’ por debajo de la LT (V-) y su proyección C’ por encima de la LT (H-).
El punto D, del IV cuadrante (cota - y alejamiento +) hace que sus proyecciones D’ y D’’ queden por debajo de la LT(H+).
El punto E con cota cero pertenece al semiplano H+ y el punto F con alejamiento cero al semiplano vertical V+ por lo que ambos se representan en diédrico a partir de la LT.