SISTEMA DIÉDRICO

Síntesis del Sistema diédrico

Unidad 6

3• REPRESENTACIÓN DE LA RECTA

3.1 Representación de la recta
En el sistema diédrico una recta del espacio vendrá dada, al menos, por dos proyecciones: la horizontal r’ y la vertical r’’. En ocasiones, será necesario representar la tercera proyección r’’’ (sobre un plano de perfil), como recurso para definir con claridad su porción en el espacio. En la imagen se representa la recta r dada por los puntos A y B situados en el I y IV cuadrante respectivamente.

3.2 Criterio de pertenencia de punto a recta.
Todo punto perteneciente a una recta, tiene sus proyecciones sobre las proyecciones correspondientes de dicha recta.

3.3 Trazas y cuadrantes de paso: partes vistas y ocultas de una recta.
Se llaman trazas de una recta a los puntos de intersección de dicha recta con los planos de proyección. Si la recta se designa por r (r’-r’’ ), llamamos R1 (R’1-R’’1) y R2 (R’2-R’’2) a sus puntos traza con el plano horizontal y vertical respectivamente. Una recta tiene como máximo dos trazas (si pasara por tres cuadrantes). Si una recta es paralela a un plano de proyección tendrá una sola traza (pasando por dos cuadrantes). Si la recta es paralela a la LT no tendrá ninguna traza

3.4 Puntos de intersección de la recta con los planos bisectores.
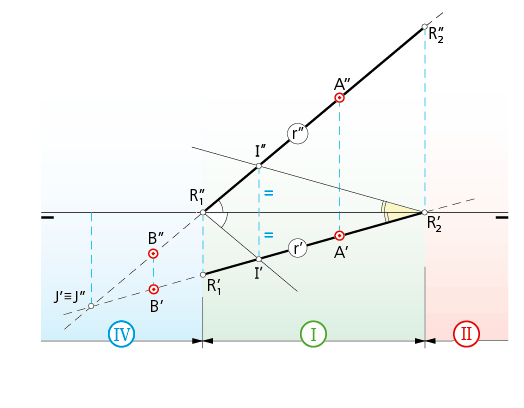
Como puede verse en la ilustración de la derecha el punto de intersección J (J’-J’’ ) de la recta con el segundo plano bisector resulta ser el punto común a sus dos proyecciones diédricas: punto con igual cota que alejamiento, en valor absoluto. Por análogo razonamiento, el punto I (I’-I’’ ) es el de intersección de la recta con el primer bisector, y queda determinado trazando rectas que partiendo de los puntos de corte de las proyecciones con la línea de tierra, formen ángulos iguales con ellas.

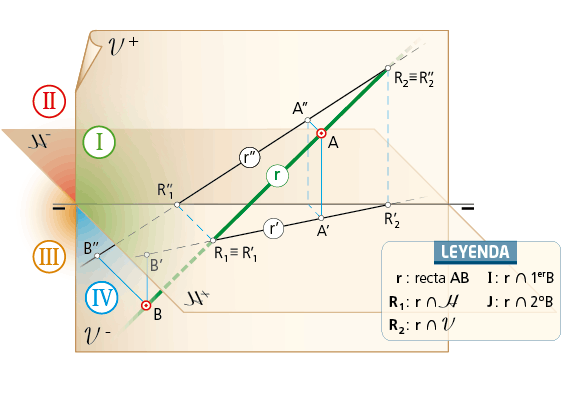
Para determinar los puntos traza se secuencian las dos proyecciones principales de la recta hasta sus puntos de corte con la linea de tierra: en esa vertical se localizan dichos puntos.

En la representación diédrica, supuestos opacos los planos de proyección H y V, se representa en linea continua el segmento de recta perteneciente al primer diedro, el resto se dibuja con línea discontinua.

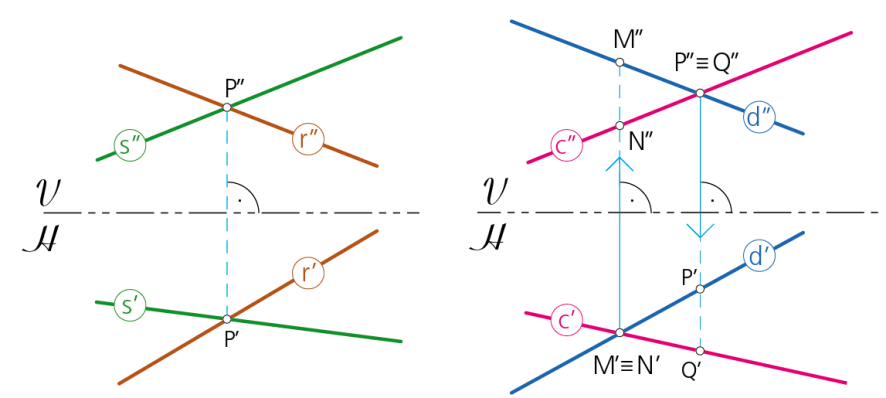
Posiciones relativas de dos rectas.

Dos rectas r y s se cortan en un punto P (común a ambas) cuyas proyecciones diédricas P’ y P’’ se encuentran en la misma línea de referencia. Pero si los puntos aparentemente comunes de las proyecciones de dos rectas no se encuentran en la misma línea de referencia, las rectas se cruzan en el espacio pero no se tocan entre sí. Por ejemplo, los puntos P y Q parecen coincidir en la proyección vertical (P’’ Q’’) pero no coinciden sobre la proyección horizontal. Idem en los puntos M y N que, coincidiendo sobre la proyección horizontal, no lo hacen sobre la vertical.