FUNDAMENTOS GEOMÉTRICOS
Transformaciones geométricas
Unidad 2
Una transformación es el resultado de un cambio (de posición, forma, tamaño…) producido en una forma geométrica. Las correspondencias entre elementos de ambas formas originan los diferentes tipos de transformaciones.
Por tanto, las formas planas pueden ser transformadas en otras, mediante la aplicación de diversos criterios que relacionan geométricamente, de alguna manera, a ambas figuras. La relación entre dichas figuras puede atender a su disposición en el plano (criterios gráficos), caso de la traslación, el giro o la simetría, o a su forma (criterios métricos) caso de la igualdad, la equivalencia y la homotecia.
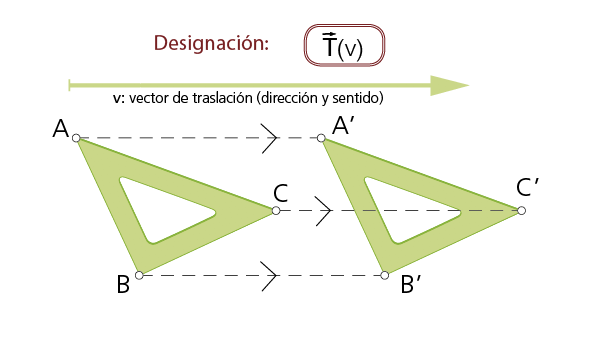
1.1 Traslación
«Trasladar una figura plana es aplicar a la misma un movimiento rectilíneo según una dirección determinada».
El vector guía v (vector de traslación) marca la dirección, el sentido y la magnitud del desplazamiento (AA’, BB’, …).
Una traslación, determinada por el vector v, transforma un punto A en otro A’ tal que el vector AA’=v. Los segmentos homólogos conservan su longitud y dirección, las rectas se mantienen paralelas y los ángulos homólogos se conservan iguales.
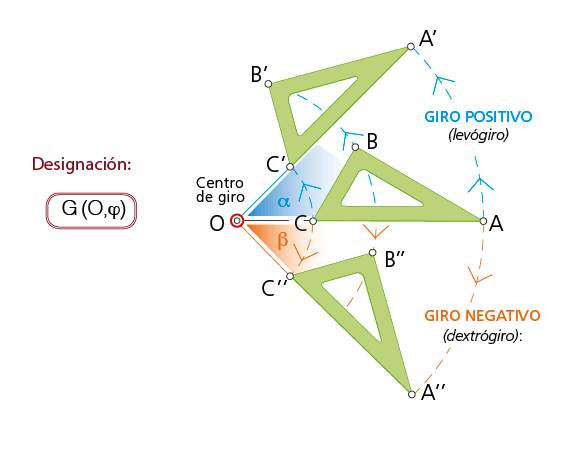
1.2 Giro o rotación
«Girar es variar la posición de una figura respecto de la inicial, aplicándole un movimiento de rotación respecto a un punto fijo O, llamado centro de giro o de rotación». Dicho centro (O) puede estar situado en el interior, en el contorno o en el exterior de la figura a transformar. El ángulo (ϕ) de giro puede ser positivo o negativo.
Un giro determinado por el centro O y una amplitud de ángulo ϕ transforma un punto A en otro A’ tal que OA=OA’ y ángulo AOA’=ϕ.
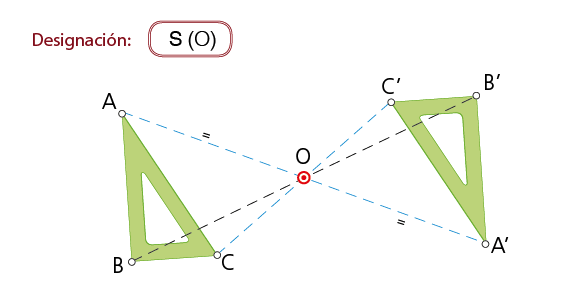
1.3 Simetría central
«Es el movimiento que corresponde a un giro, cuyo ángulo ϕ vale 180° (dextrógiro o levógiro), con centro de rotación (O)».
En una simetría central, dos puntos simétricos se encuentran alineados y son equidistantes del centro de simetría O. Los segmentos simétricos resultan ser paralelos (AB // A’B’ ).
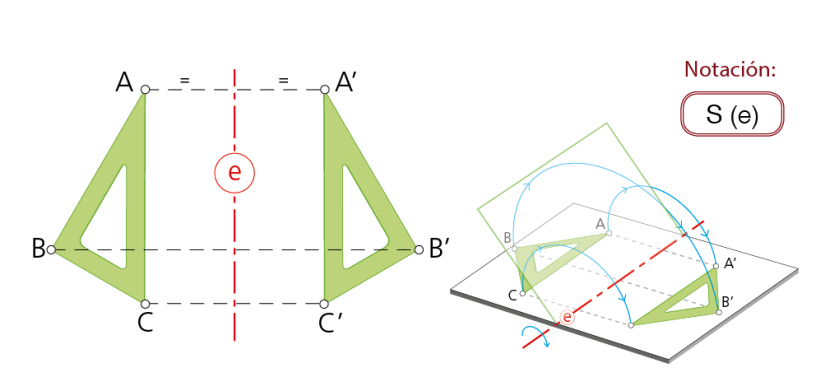
1.4 Simetría axial
«Es el movimiento que corresponde a una figura que se separa del plano que la contiene para volver a él mediante una semirrotación alrededor de una recta fija (e) del plano inicial, llamada eje de simetría».
Una simetría determinada por el eje e, transforma un punto A en otro A’ tal que dicho eje es la mediatriz del segmento AA’.

1.5 Movimientos directos e inversos.
Su vértice es exterior a la circunferencia y sus lados son secantes o tangentes a ella.
Su valor es igual a la semidiferencia de los ángulos centrales que abarcan sus lados.

1.6 Producto de movimientos.
La aplicación sucesiva de dos o más movimientos (traslaciones, giros y simetrías) es otro movimiento y se denomina producto de movimientos.El resultado es una figura «imagen» igual a la «original»; únicamente puede cambiar su posición en el plano.
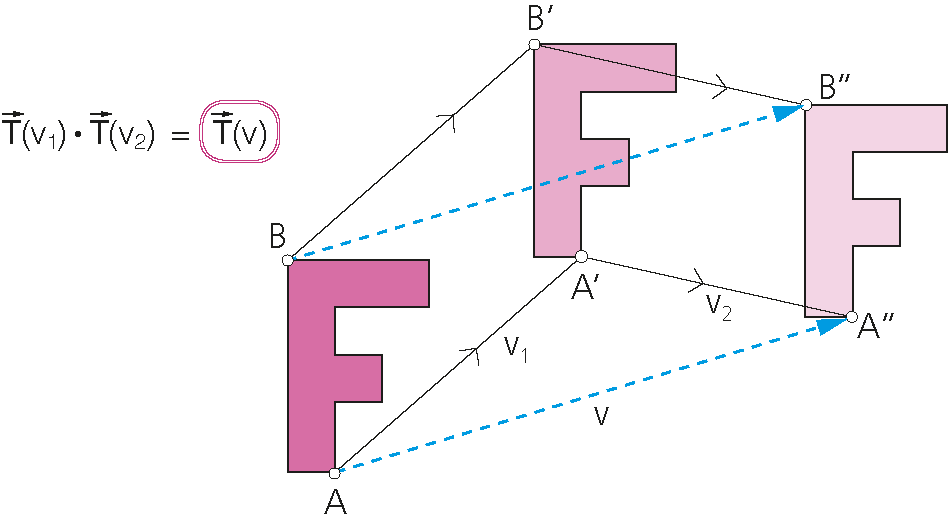
Producto de dos traslaciones.
El producto de dos traslaciones, de vectores v1 y v2, es otra traslación de vector v
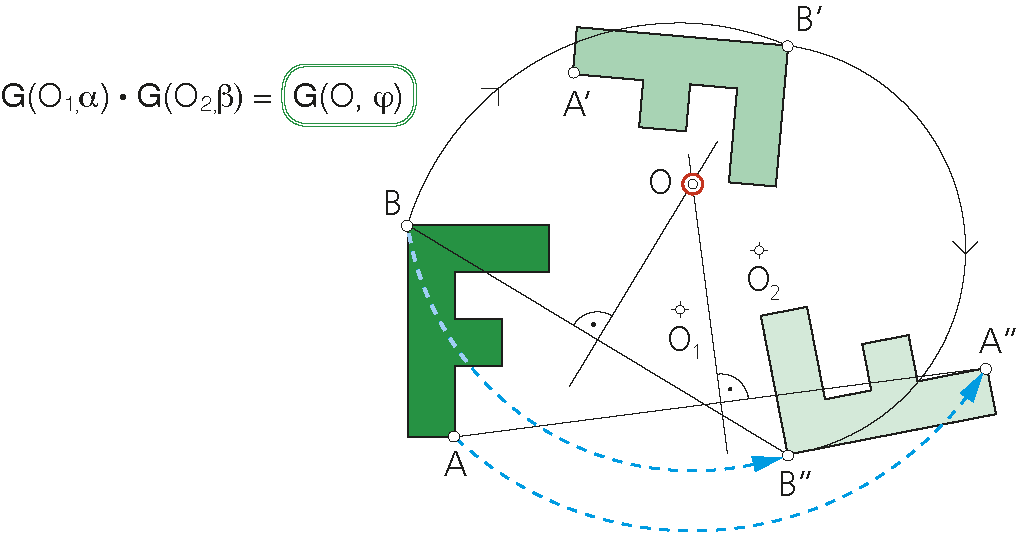
Producto de dos giros.
El producto de dos giros es otro giro, de centro la intersección de las mediatrices de los segmentos que unen puntos homólogos de las posiciones inicial y final.
Cuando las rectas mediatrices son paralelas, el producto es una traslación.
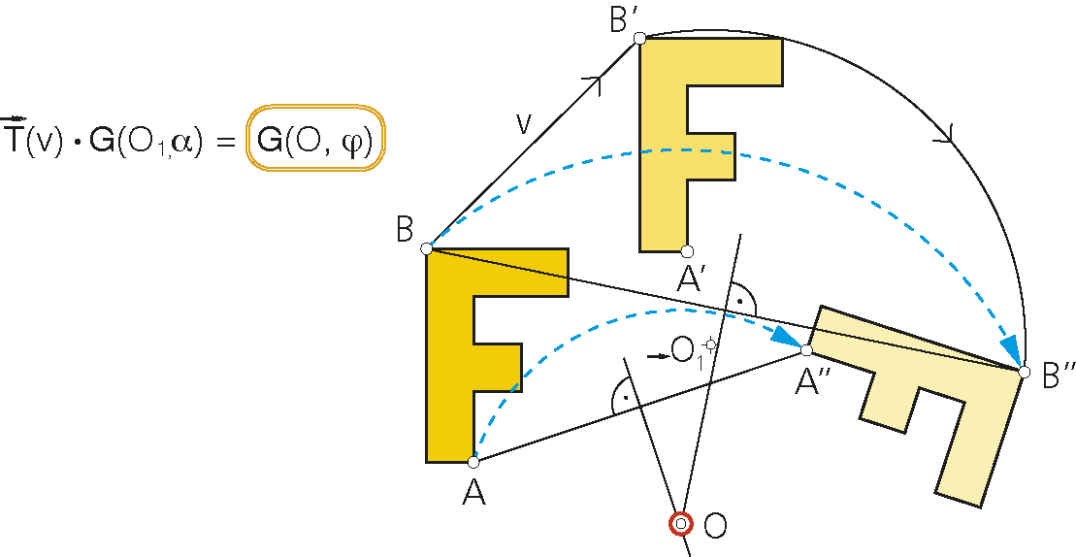
Producto de una traslación por un giro.
El producto de una traslación por un giro (o viceversa) es un giro cuyo centro se determina como en el caso anterior; ya que una traslación es un giro de centro impropio.
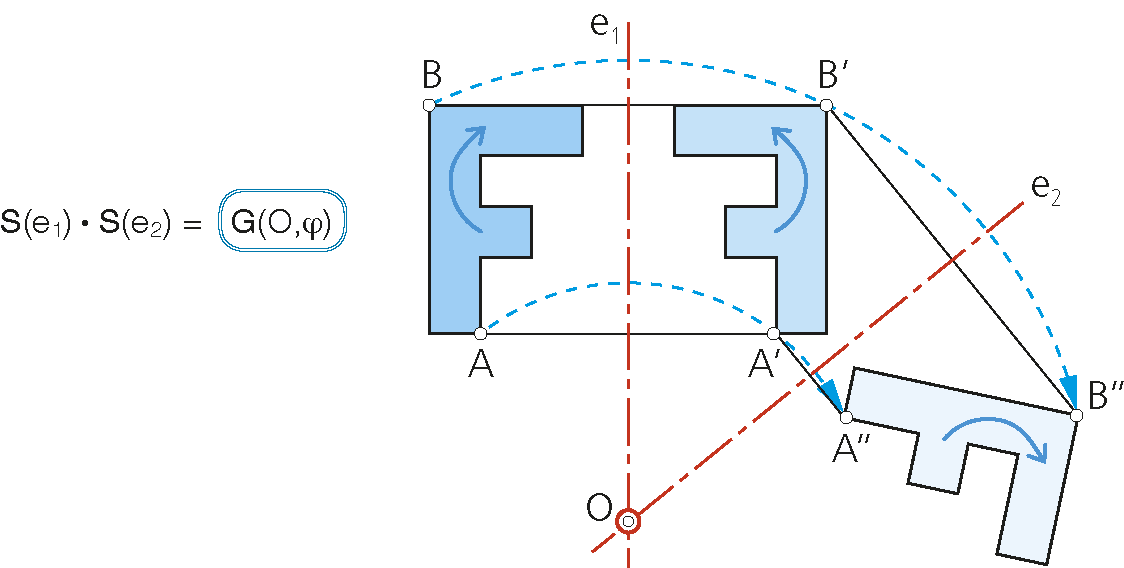
Producto de dos simetrías axiales.
El producto de dos simetrías axiales es un giro, cuyo centro es el punto intersección de los ejes de simetría. Si ambos ejes son paralelos el producto resulta ser una traslación, o lo que es lo mismo, un giro de centro impropio.
CONCLUSIONES GENERALES
• El producto de dos movimientos directos o inversos es otro movimiento directo.
• El producto de un movimiento directo por otro inverso invierte el sentido entre la figura inicial y la imagen final, las cuales no pueden relacionarse entre sí por un solo movimiento, a no ser se trate de casos particulares.