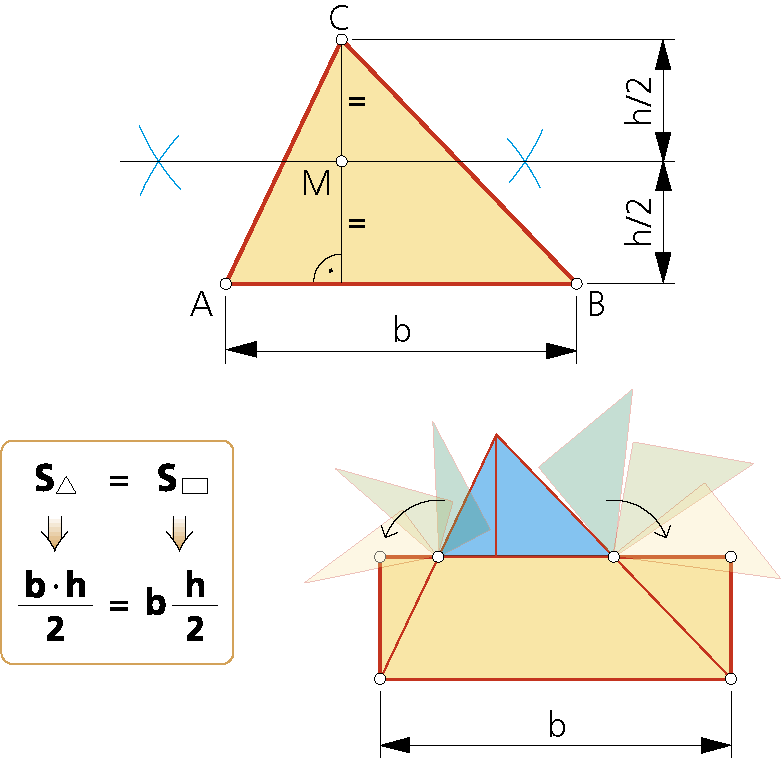FUNDAMENTOS GEOMÉTRICOS
CONTENIDO COMPLEMENTARIO
Unidad 2
LA DIVINA PROPORCIÓN
Divina proporción o proporción áurea es el nombre que se dió en el siglo XIX a una concreta proporcionalidad obtenida mediante la división de un segmento en lo que Euclides llamó media y extrema razón. Éste la definía así: «se dice que un segmento recto ha sido dividido en media y extrema razón cuando el segmento está dividido en dos partes, de modo que una de ellas –el áureo– es la media proporcional entre todo el segmento y la parte restante».
Para ello, basta situar un punto C del segmento AB de forma que se verifique:
La razón de esta proporción (a/m = Φ) nos resulta a los humanos especialmente armoniosa.
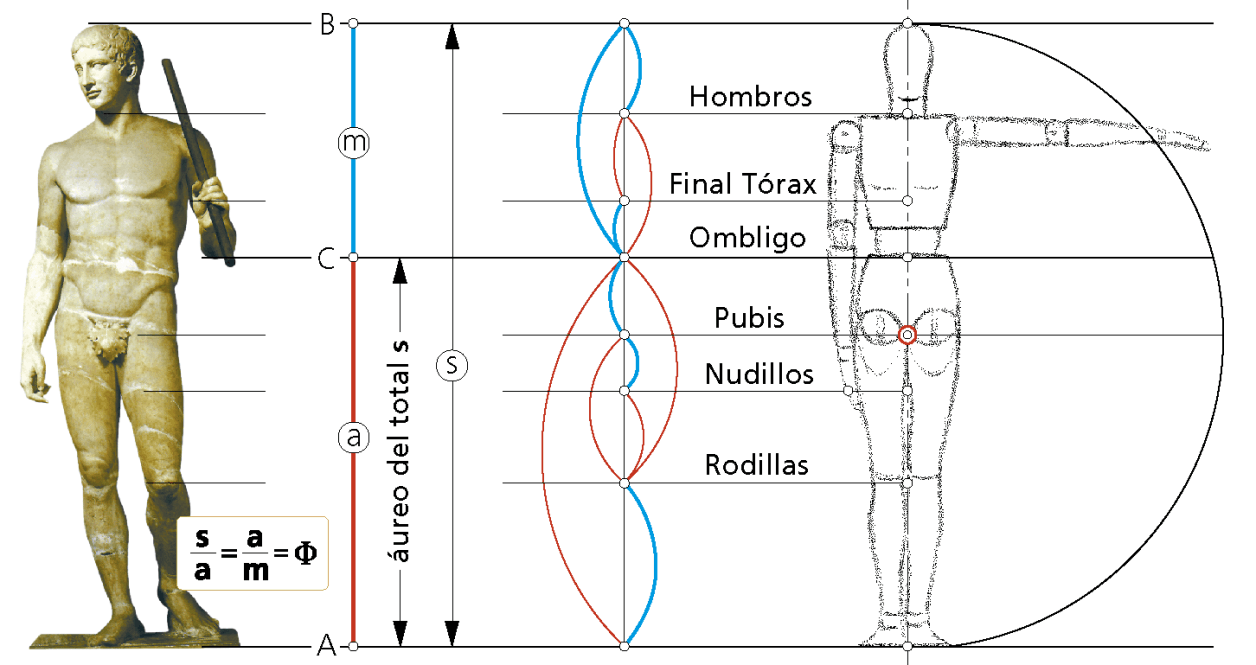
El cuerpo humano y la divina proporción.
Hacia 1850, Adolf Zeising (1810-1876), Profesor de filosofía en Munich, contrastó estadísticamente que el ombligo divide la altura total del cuerpo en la proporción áurea; asimismo cada una de estas partas origina a su vez secciones áureas entre zonas concretas del cuerpo.
Ya era conocida en la Grecia antigua, pues aparece en algunos de sus templos y edificios. Se designa con la letra griega Φ (fi) en honor al arquitecto Fidias.
Los artistas del Renacimiento la tuvieron muy en cuenta en sus obras. Leonardo da Vinci lo llamó el Número de Oro y a la razón Sección Áurea, y su amigo Fray Luca Paccioli (1509) lo menciona en sus escritos como la Divina Proporción.
Para ellos, el cuerpo humano perfecto era el que poseía esa proporción entre la altura y la distancia del ombligo al suelo, como se muestra en la ilustración de arriba.
Si en la expresión (*) se dividen los términos de la primera razón por m, la fracción no varía, obteniendo:
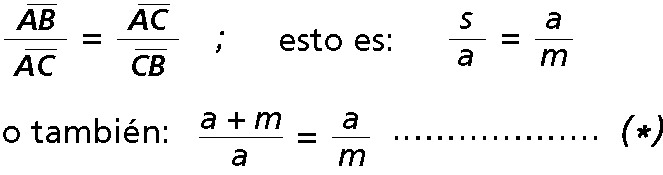
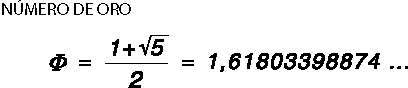
Este número ha sido, a la vez, símbolo cosmológico, fórmula mágica y clave de diversas construcciones geométricas utilizadas, sobre todo, en arquitectura. Su presencia en los elementos de la naturaleza es constante y arquitectos, escultores y pintores de todos los tiempos han utilizado esta proporción como método de composición de sus obras, al observar en ella una agradable impresión de armonía y belleza. Se dan ejemplos en bastantes obras de la arquitectura griega, como es el caso de «El Partenón» en Atenas y, más recientemente, en la obra del arquitecto francés Le Corbusier. Pintores de relevante talento como Miguel Ángel en «La Sagrada Familia» o Velázquez en «Las Hilanderas» también utilizaron las posibilidades estéticas de la proporción áurea.

LE CORBUSIER (1887-1965) «Modulor», 1953.
El modulor es un sistema de medida ergonómico, basado en la relación de medidas a través del número áureo para viviendas, espacios y arquitecturas en general.

FIDIAS (500-431 a.C.) «El Partenón», 438 a.C.
Este famoso templo de la acrópolis de Atenas es un buen ejemplo de proporción áurea entre sus elementos arquitectónicos. Además se aplica en su construcción «el entasis»: un ideal geométrico griego entre proporciones que evita la desvirtuación por efectos ópticos de distancia o puntos de vista.
LA EQUIVALENCIA O LA IGUALDAD AÉREA
La RAE define el concepto de equivalencia geométrica cuando dos figuras planas o dos sólidos con formas distintas tienen iguales respectivamente sus áreas (entendida ésta como la medida de la extensión de su superficie) o sus volúmenes.
Es un concepto distinto pero intrínsecamente relacionado con los conceptos de proporción y semejanza mostrados en esta Unidad Didáctica. Para entender este concepto con mayor facilidad vamos a proponer ejemplos de equivalencia entre formas geométricas simples.
TRIÁNGULOS EQUIVALENTES
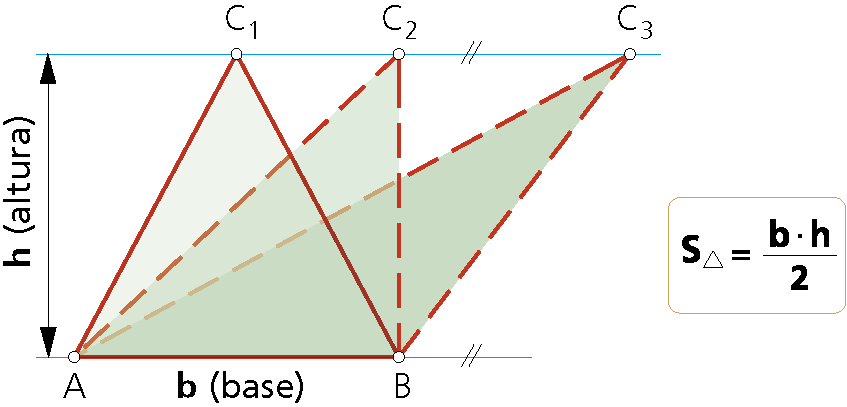
«Dos triángulos de iguales bases y alturas son equivalentes».
El triángulo ABC1, de altura h, es equivalente a los ABC2, ABC3, …, que poseen la misma base (AB=b) e igual altura (h), dado que el área de todos ellos es: b·h/2.
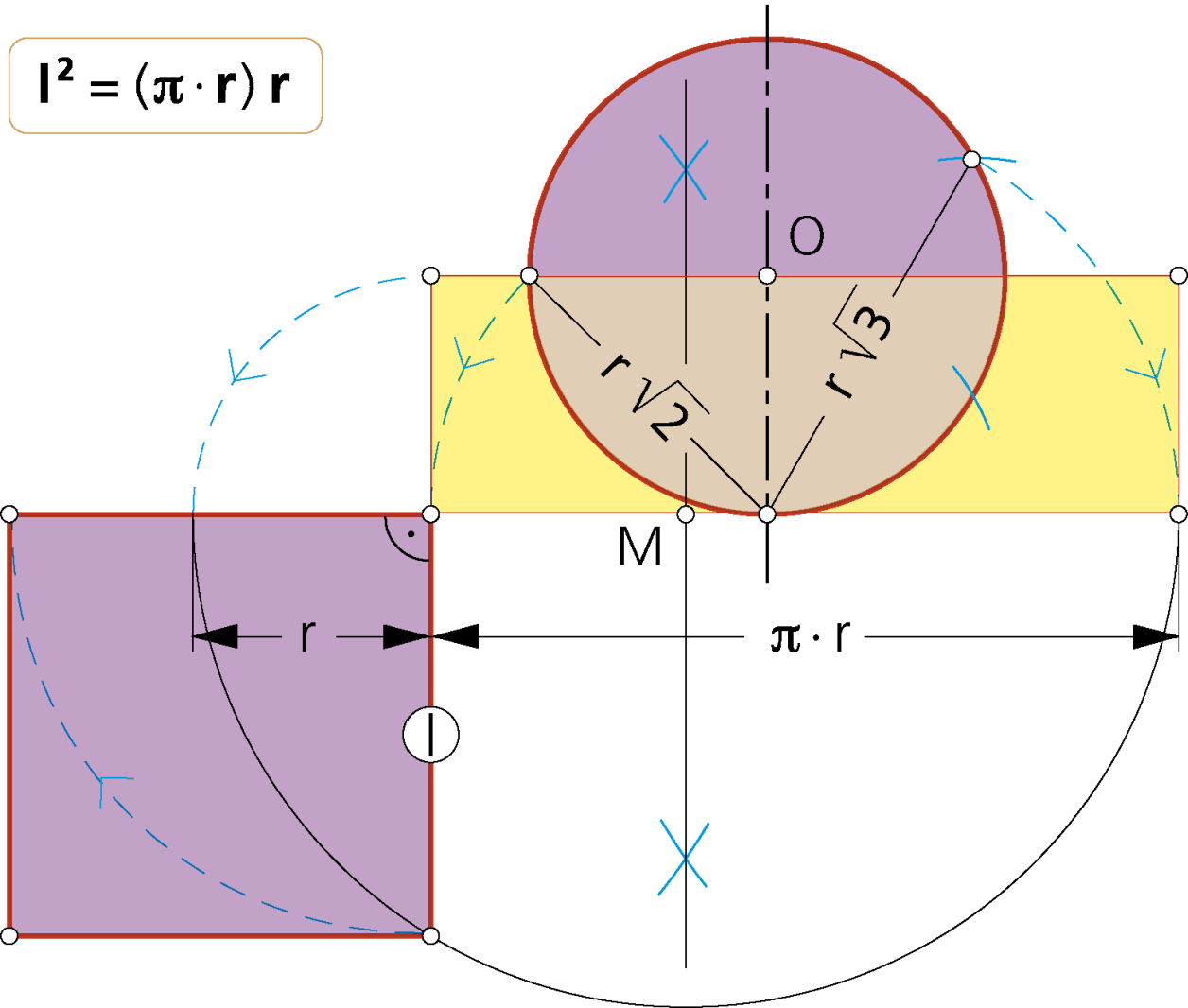
CUADRATURA APROXIMADA DEL CÍRCULO
La dificultad de resolver, con exactitud, el problema de construir con las herramientas euclidianas –regla y compás–
un cuadrado equivalente a un círculo dado, radica (al igual que sucede con su rectificación) en que π es un número «trascendente», esto es, no puede ser raíz de ninguna ecuación matemática de coeficientes racionales.
Admitiendo como suficientemente precisa la rectificación de la circunferencia (en términos gráficos), el problema de la cuadratura del círculo equivale a construir un segmento de magnitud igual a π, dado el segmento unidad.
– Igualando áreas: π·r2 = l2 ; (π·r) r = l2. Por tanto, si suponemos un rectángulo de base (π·r) y altura igual al radio r, éste sería equivalente al círculo y basta con construir el cuadrado equivalente a dicho rectángulo; para ello, como siempre, se halla la media geométrica entre sus dos dimensiones (π·r) y r.
RECTÁNGULO EQUIVALENTE A UN TRIÁNGULO
«Un triángulo cualquiera puede siempre transformarse en un rectángulo de igual base y mitad altura, o de base mitad e igual altura».
– Se determina el punto medio M de su altura (trazando la mediatriz) y, por él, se traza la paralela a la base. El rectángulo de base la del triángulo dado y altura su mitad, equivaldrá al triángulo original; sus áreas son iguales: S = b·h/2.
– En la equicomposición de ambas figuras, para formar la final se añaden las mismas subformas que se retiran a la figura original.