dos

2- HOMOTECIA

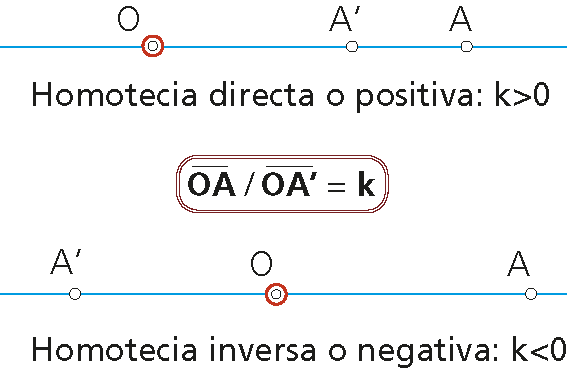
Dado el punto fijo O y un número real k≠ 0, se llama homotecia a la transformación geométrica que hace corresponder a un punto A otro A’, alineado con A y con O, tal que:
OA/OA’ = k (cte.)
Al punto O se le denomina centro de homotecia, y a la constante k razón de la homotecia.
Designación: H (O,k).
-Si k>0: A y A’ están del mismo lado que O. La homotecia se dice que es directa o positiva. -Si k<0: A y A’ están a distinto lado que O. La homotecia se dice que es inversa o negativa.

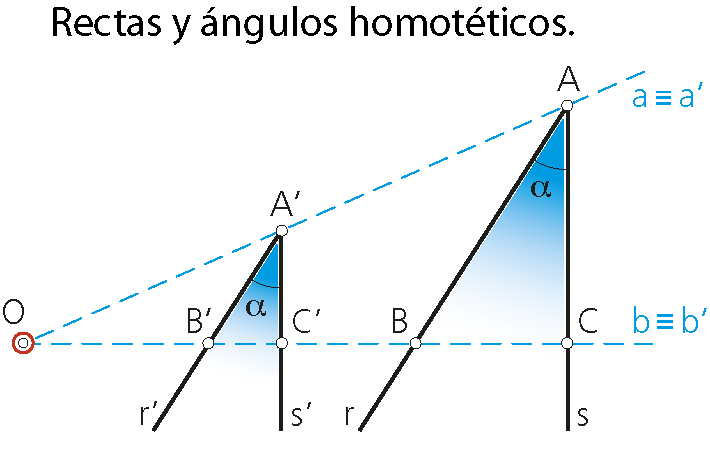
2.1 Propiedades de la homotecia

Una recta r que no pasa por el centro O de homotecia se transforma en otra r’ paralela. Existe proporcionalidad (Teorema de Tales) entre los triángulos OAB y OA’B’.
• La razón entre dos segmentos homólogos es igual a la razón de homotecia. Esto es: OA’/OA=OB’/OB=AB’/A’B=…=k.
• Las rectas que pasan por el centro O se transforman en sí mismas (son dobles). En la fig. de la derecha, las rectas a y b son dobles.
• Los ángulos homólogos son iguales, ya que sus lados son paralelos:
ángulo BAC = ánguloB’A’C’=a.

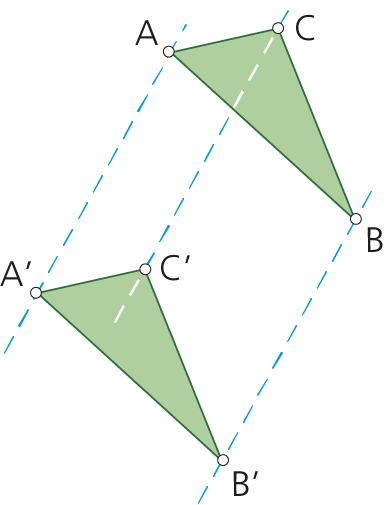
Propiedad sobre la transformación : TRASLACIÓN

• Si el centro de homotecia se encuentra en el infinito (homotecia impropia) y la razón k=1, la correspondencia geométrica se transforma en una TRASLACIÓN.

Propiedad sobre la transformacion : IDENTIDAD

• Si la razón de homotecia es igual a la unidad (k=1), todos los puntos del plano son dobles (homólogos de sí mismos) y la transformación es una IDENTIDAD

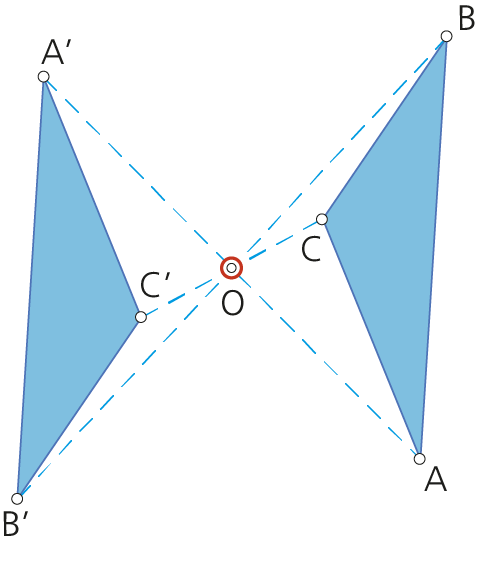
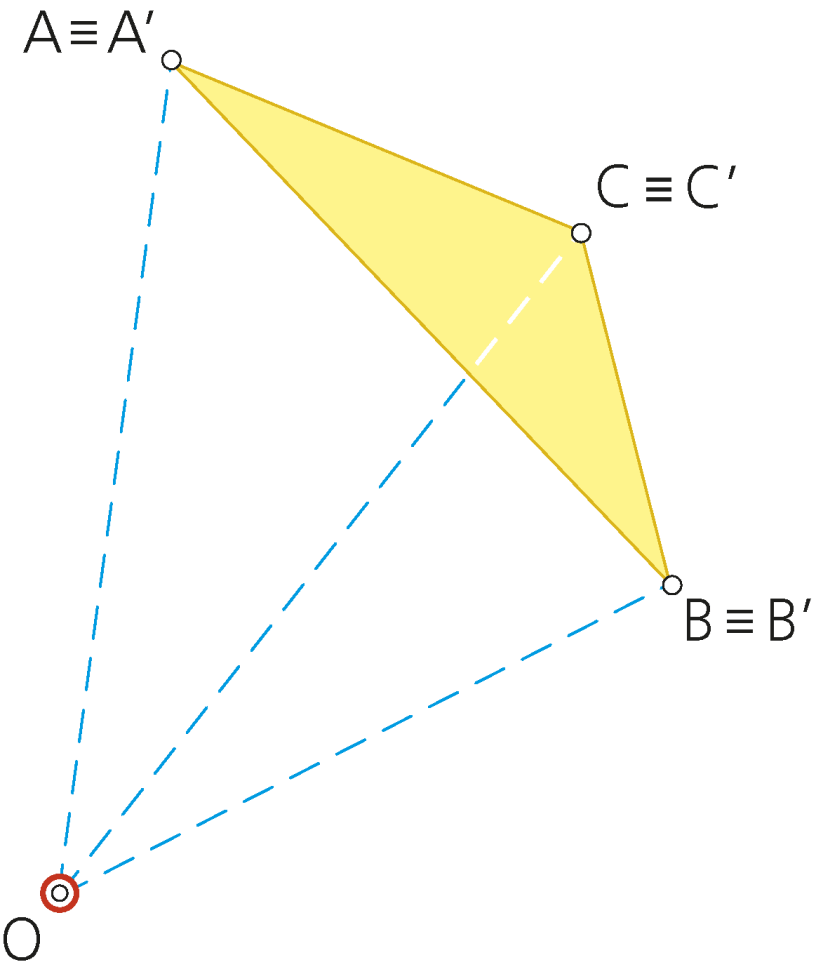
Propiedad sobre la transformación : SIMETRIA CENTRAL

• Si la razón de homotecia es k=-1, la transformación es una SIMETRÍA CENTRAL de centro O.

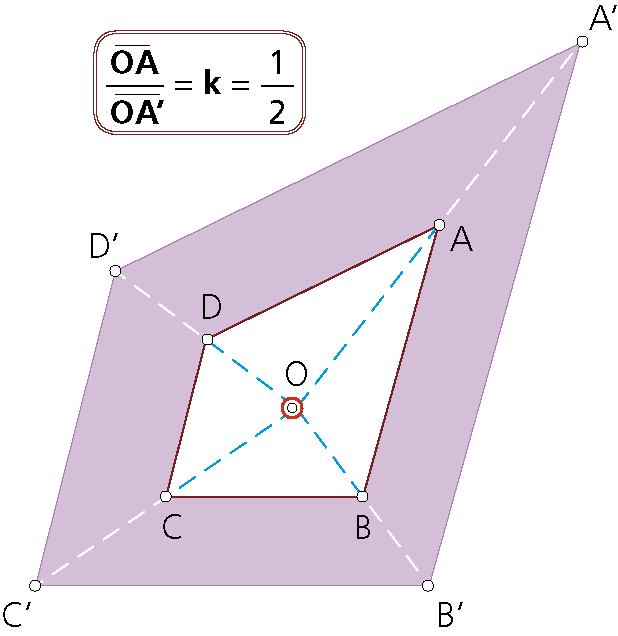
2.2 2 Trazado de figuras homóticas

Para dibujar una figura homotética de otra, puede elegirse como centro de homotecia (O) cualquier punto interior a la figura, exterior o del contorno de la misma. Analicemos cada caso con un ejemplo.

Con el centro O en un punto interior al polígono.

Datos: cuadrilátero ABCD; centro de homotecia O (en el interior de la figura) y razón de homotecia: k=1/2.

Construcción: Se define A’ como punto homotético de A, verificándose: OA/OA’=k=1/2; OA’=2OA.
Partiendo de conocer la posición del punto A’ se trazan paralelas a los lados y se determina
el polígono homotético A’B’C’D’.

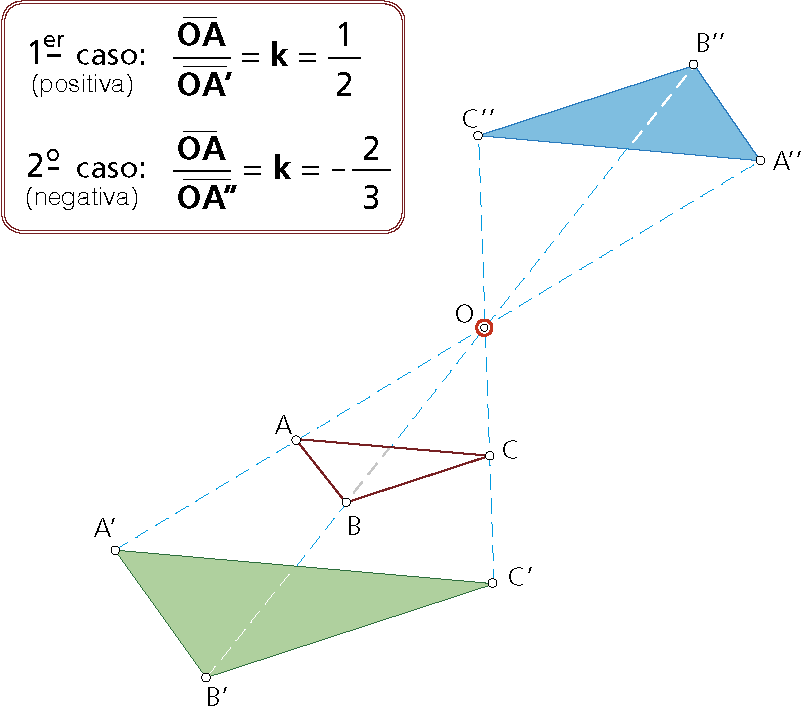
Con el centro O en un punto exterior al polígono ABC.

Datos: triángulo ABC; centro de homotecia O (en el exterior de la figura) y razón de homotecia en los dos casos posibles, que se muestran en la imagen.

Construcción: Se determina A’ como homotético de A, cumpliéndose que OA’=2OA. Seguidamente, se trazan paralelas a los lados homólogos hasta completar el triángulo homotético del dado.
Análogamente, el vértice A’’ se obtiene considerando que OA’’=3OA/2. El resto de vértices que determina la figura homotética se consigue trazando, como siempre, paralelas por el punto A’’ previamente determinado.

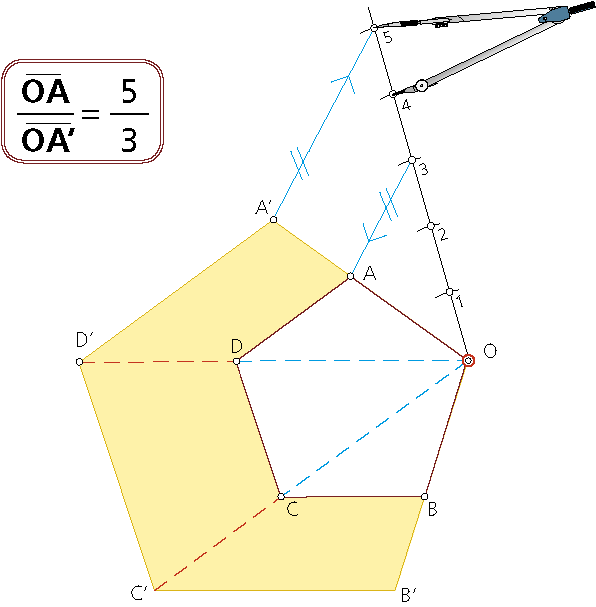
Con el centro O en un vértice de la forma.

- Datos: pentágono OABCD; centro de homotecia en el punto O (vértice de la figura)
y razón de homotecia: k=5/3.

Construcción:
Como en casos anteriores, se comienza por determinar el homotético de un vértice (en la figura A’) que verifica la relación: OA/OA’=5/3. Como siempre, una vez determinado A’ se trazan paralelas a los lados homólogos, determinando el polígono homotético OA’B’C’D’.

FUNDAMENTOS GEOMÉTRICOS

Homotecia