FUNDAMENTOS GEOMÉTRICOS
Semejanza entre figuras
Unidad 2
4- SEMEJANZA ENTRE FIGURAS
«Dos figuras son semejantes, cuando sus magnitudes lineales son proporcionales y sus magnitudes angulares son iguales; es decir, dos polígonos son semejantes si sus lados son proporcionales y sus ángulos iguales».
La semejanza de figuras se fundamenta en el Teorema de Tales, en donde se estableció la proporcionalidad entre segmentos de rectas paralelas al ser cortadas por rectas concurrentes.
Las formas poligonales ABCDE y A’B’C’D’E’ son semejantes (ver fig. inferior); es decir, se puede determinar una relación entre ambas figuras tal que a cada punto de una corresponde un punto de la otra, y que los segmentos definidos por dos puntos que se corresponden en ambas figuras guardan una relación de proporcionalidad constante k: razón de semejanza.
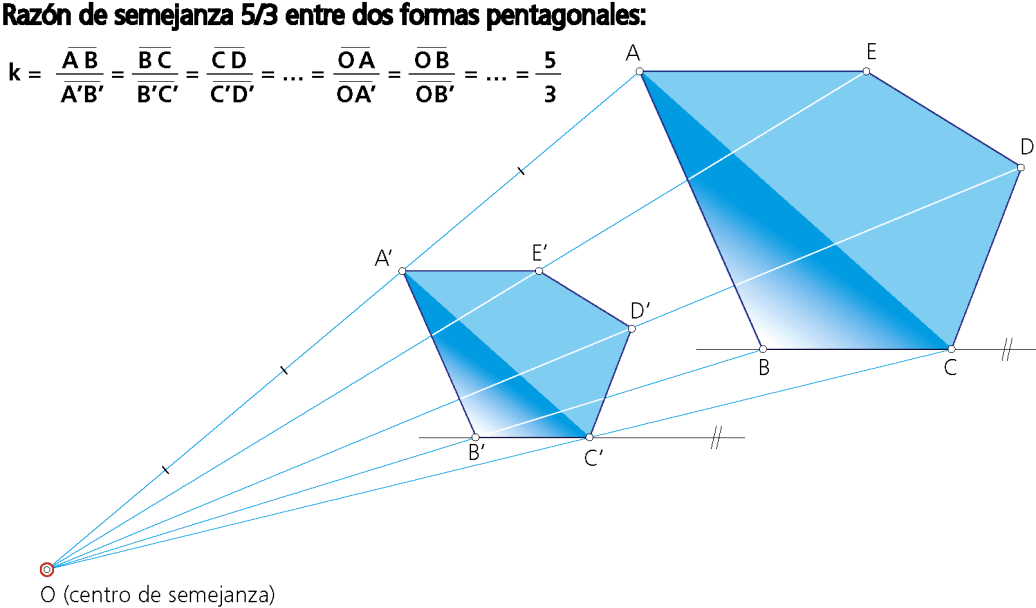
Los elementos que se corresponden (lados, diagonales,vértices y ángulos) son los denominados elementos homólogos. Así, los vértices homólogos de A, B, C… son A’, B’, C’…; a su vez, los lados homólogos serán aquéllos que unen vértices homólogos, tales como AB y A’B’.
La relación de semejanza implica igualdad de ángulos formados por segmentos homólogos.
La relación de igualdad de ángulos implica lógicamente que dos polígonos regulares de igual número de lados son siempre semejantes.
En resumen, dos figuras son semejantes cuando tienen la misma forma y distinto tamaño.
En los polígonos presentados la razón de semejanza k es igual a 5/3, y por tanto, la forma poligonal ABCDEA será mayor que su semejante A’B’C’D’E’A’.
La semejanza de polígonos se fundamenta en la de los triángulos, según la cual, dos triángulos son semejantes (figura anterior, ABC es semejante a A´B´C´)cuando tienen sus tres ángulos iguales y sus lados y rectas notables (alturas, medianas, bisectrices,…) proporcionales; es decir, cuando cumplen alguno de los siguientes criterios de semejanza:
• Cuando tienen dos ángulos iguales.
• Cuando tienen un ángulo igual y proporcionales los lados que lo forman.
• Cuando tienen los tres lados proporcionales.

Maqueta interactiva del proyecto Nuevo Norte Madrid.
Es frecuente que los diseñadores, arquitectos, urbanistas y técnicos en general preparen los proyectos de sus obras en dimensiones reducidas como paso previo a su construcción.Para ello, se ayudan de planos y maquetas. Unos y otros trabajan en sus respectivas obras con formas iguales, pero de distinto tamaño, esto es, con formas semejantes.
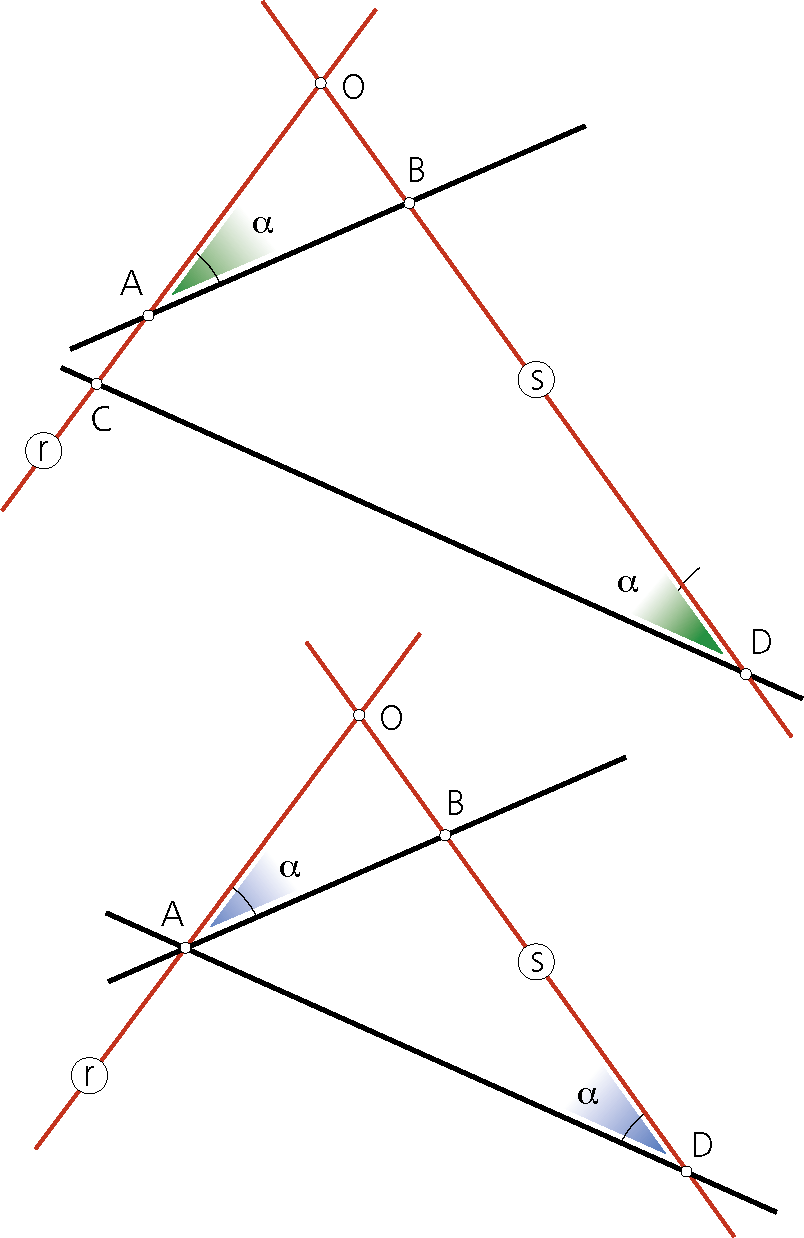
RECTAS ANTIPARALELAS
«Dos rectas AB y CD se dice son antiparalelas respecto de otras dos r y s cuando el ángulo a que forma la recta AB con la recta r es igual al ángulo que forman la recta CD con la recta s». Los triángulos OAB y OCD (figura al pie-superior) son semejantes por tener los tres ángulos iguales y, por tanto, se verifica: OA/OD=AB/CD=OB/OC.