SISTEMA DIÉDRICO II
Síntesis del Sistema diédrico
Unidad 7
2• INTERSECCIÓN DE RECTA Y PLANO
La intersección de una recta r con un plano α, no paralelo a la recta, obviamente, es un punto. Si por una recta r se hace pasar un plano cualquiera π (en el sistema diédrico preferentemente un plano proyectante) y, se halla la recta intersección i del plano α con el plano π (según se muestra en la ilustración), el punto común de la recta i con la r determina el punto intersección I de ésta con el plano α.
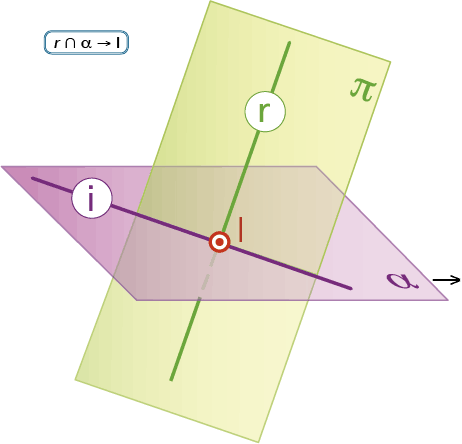
En los ejercicios de intersección de recta y plano se supone que el plano es opaco; lo que trae consigo que a partir del punto común de la recta con el plano, ésta quede oculta (o se muestre en linea discontinua).
El análisis de la posición relativa de la recta y el plano, permite determinar la visibilidad de la recta en proyección.
Este análisis se efectúa mediante la observación de las coordenadas relativas de un punto de la recta, aparentemente común con el plano. Así, para analizar partes vistas y ocultas en la proyección vertical (alzado), se verifica su correspondencia de alejamientos relativos sobre la proyección horizontal (planta): será visto el elemento geométrico más próximo al observador. Paralelo análisis cabe realizar para obtener partes vistas y ocultas en la proyección horizontal (planta), pero ahora verificando su correspondencia relativa de cotas en la proyección vertical (alzado).
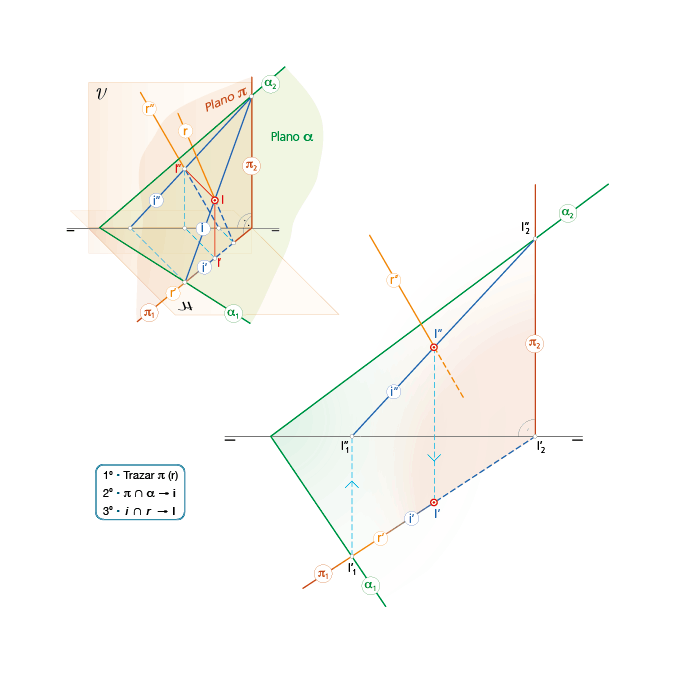
2.1 Intersección de recta y plano dado por sus trazas.
En diédrico, por su facilidad de uso, se hace pasar por la recta r, indistintamente, un plano proyectante horizontal o bien un plano proyectante vertical. La recta i, intersección de π con α, corta a la recta r en el punto I buscado.