SISTEMA DIÉDRICO II
Síntesis del Sistema diédrico
Unidad 7
3• PARALELISMO
Todas las construcciones que se llevan a cabo en diédrico para la resolución de problemas o para comprobaciones de paralelismo entre rectas, planos o rectas y planos, se basan en cuatro propiedades fundamentales del espacio.
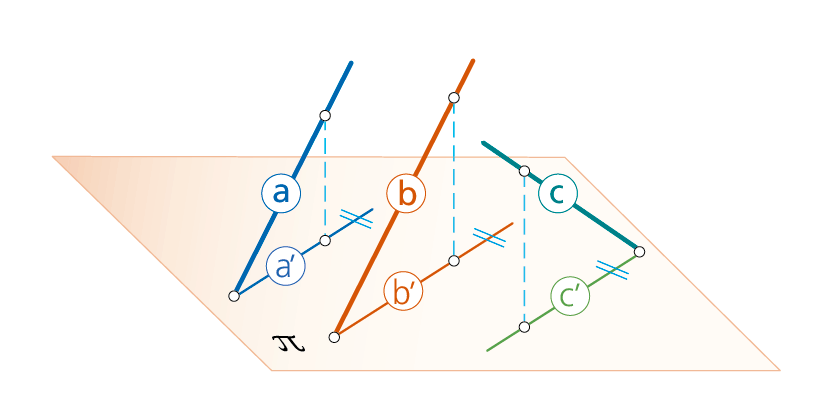
3.1 Paralelismo entre rectas. Fundamentos. 3.1.a:
«Si dos rectas a y b son paralelas en el espacio también lo son sus proyecciones a’ y b’ sobre un plano π cualquiera». No es cierto, en cambio, lo recíproco (condición necesaria pero no suficiente), ya que aunque sean paralelas las proyecciones, por ejemplo b’ y c’ (de las rectas del espacio b y c), sobre un mismo plano π, no se puede asegurar, como se aprecia en la figura, que las rectas (b y c) lo sean.
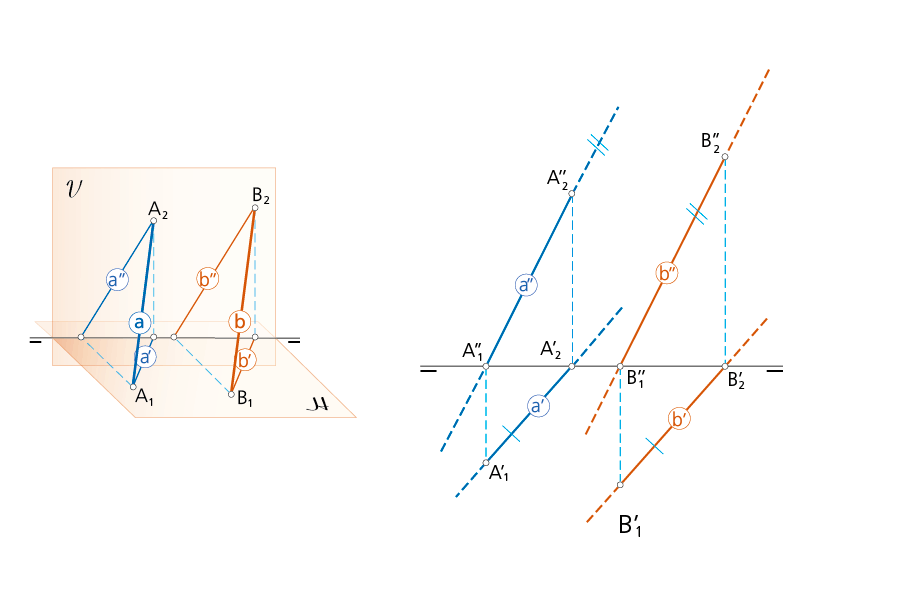
• 3.1.b:
«Cuando son paralelas las proyecciones de dos rectas sobre dos planos distintos secantes las rectas del espacio son, también, paralelas». Si la proyección a’ es paralela a la b’ y además la proyección a” es paralela a la b” las rectas a y b son paralelas. No obstante, las rectas de perfil suelen ser una excepción.
Todas ellas tienen sus proyecciones horizontales y verticales perpendiculares a la LT y, por tanto,

3.1.c:
«Si las proyecciones de dos rectas sobre un plano se superponen y las proyecciones sobre otro plano secante son paralelas, las rectas son paralelas». En este ejemplo se ve que, si la proyección e’ coincide con la proyección de d’, y además e’’ es paralela a d’’, las rectas e y d son paralelas en el espacio pero una de sus vistas diédricas es a la vez e’ y d’.
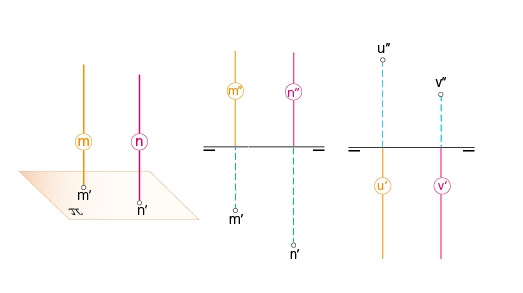
3.1.d:
«Si las proyecciones de dos rectas sobre un mismo plano se reducen a un punto, las rectas son paralelas entre si y, lógicamente, perpendiculares al plano de proyección». Esto puede verse en el gráfico a la derecha, donde las rectas m y n, donde las proyecciones sobre el plano π son los puntos m’ y n’. En diédrico, las rectas pueden ser verticales (caso de m y n) o de punta (caso de las rectas u y v).
3.2 Paralelismo entre recta y plano.
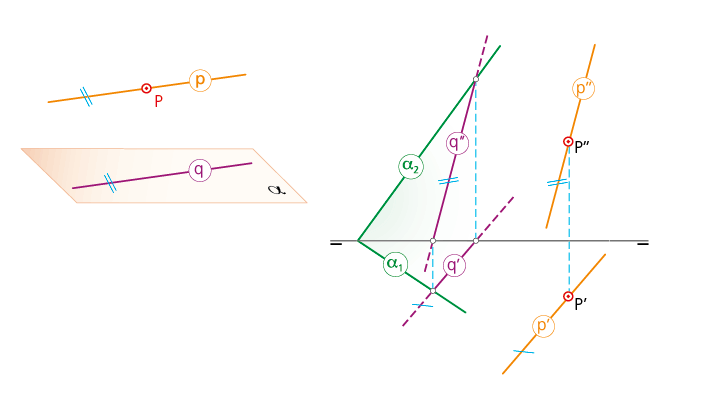
«Para que una recta sea paralela a un plano basta que sea paralela a una recta de dicho plano». En este caso, la recta p no corta al plano en ningún punto (condición de paralelismo entre recta y plano).
Esquema y representación diédrica de una recta p paralela al plano a (y a la recta q contenida en dicho plano).
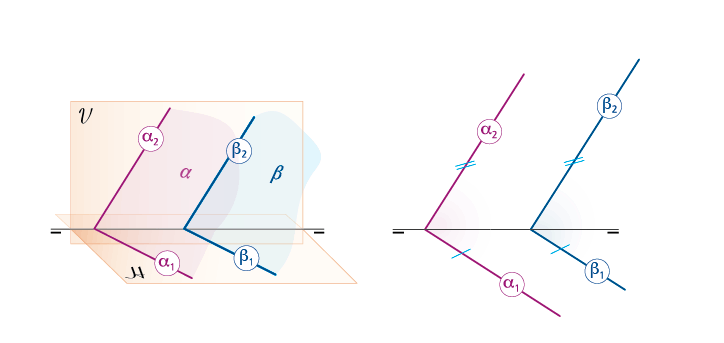
3.3 Paralelismo entre planos.
«Dos planos paralelos cortan a un tercer plano (por ejemplo H o V) según rectas paralelas». En consecuencia, en el sistema diédrico, los planos paralelos α y β tienen sus trazas homónimas paralelas: α1 paralela a β1 y α2 paralela a β2.
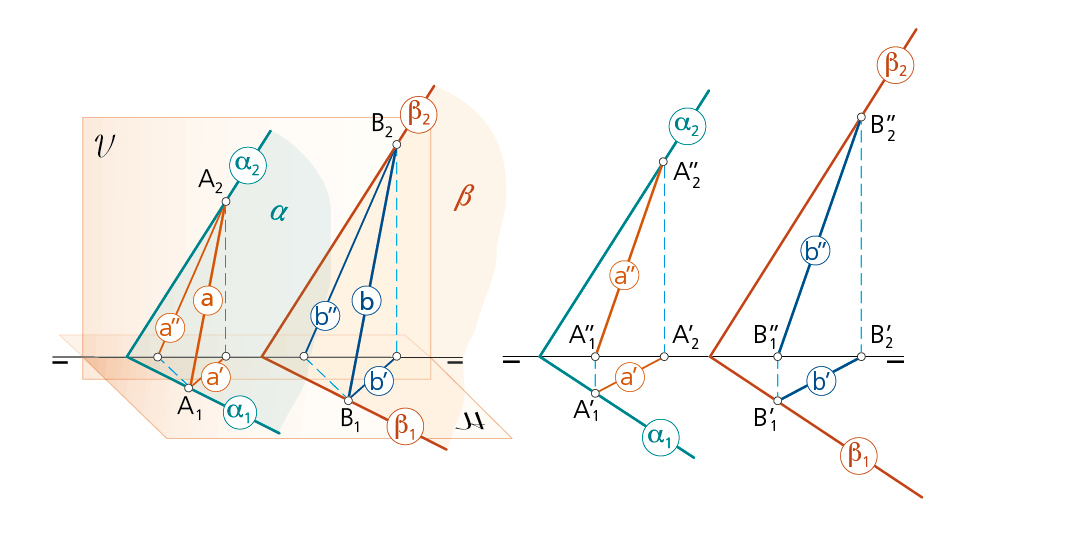
Consecuencias del paralelismo entre planos
No sólo las trazas de planos paralelos serán paralelas entre sí, sino que, además, lo serán las proyecciones de todas las rectas horizontales y frontales de ambos planos.
Nótese que, en general, las rectas contenidas en dos planos paralelos simplemente se cruzan.
Para que además sean paralelas, deben ser paralelas sus proyecciones, como se indica en la figura: a’ es paralela a b’ y a’’ es paralela a b’’, lo que significa que las rectas a y b del espacio son paralelas.