+CONTENIDO COMPLEMENTARIO

LA PROPORCIÓN AUREA
La Divina proporción o proporción áurea es el nombre que se dio en el siglo XIX a una concreta proporcionalidad obtenida mediante la división de un segmento en lo que Euclides llamó media y extrema razón. Este la definía así: «se dice que un segmento recto ha sido dividido en media y extrema razón cuando el segmento está dividido en dos partes, de modo que una de ellas –el áureo– es la media proporcional entre todo el segmento y la parte restante».
Para ello, basta situar un punto C del segmento AB de forma que se verifique: La razón de esta proporción (a/m = Φ) nos resulta a los humanos especialmente armoniosa.
Ya era conocida en la Grecia antigua, pues aparece en algunos de sus templos y edificios. Se designa con la letra griega Φ (fi) en honor al arquitecto Fidias.
Los artistas del Renacimiento la tuvieron muy en cuenta en sus obras. Leonardo da Vinci lo llamó el Número de Oro y a la razón Sección Áurea, y su amigo Fray Luca Paccioli (1509) lo menciona en sus escritos como la Divina Proporción.
Trazado si el vértice no está localizado.
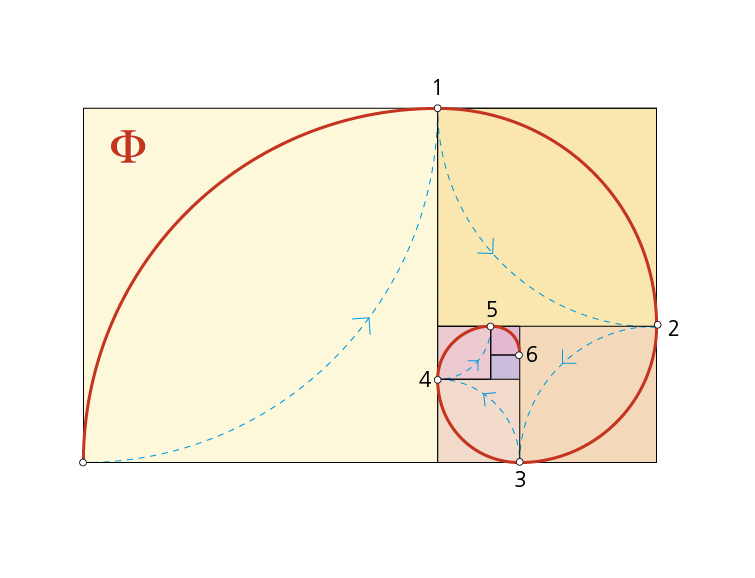
Dinamismo del rectángulo áureo. El rectángulo áureo tiene como propiedad más importante la posibilidad de efectuar una separación ilimitada de rectángulos semejantes a él, por tanto, también áureos, cada vez de menor tamaño. Además, se obtiene una espiral logarítmica, esquema base del desarrollo de los moluscos gasterópodos como el Nautilo.
Ejemplos de Proporción Aurea
Lo más fascinante de esta proporción perfecta, no es quizás toda esa parte matemática, sino la forma en la que aparece de manera constante en la naturaleza. Algunos procesos naturales, incluyendo la formación de las galaxias, algunos seres vivos, con crecimiento por agregación y rotación, siguen una forma basada aproximadamente en dicha espiral logarítmica.
Observa los ejemplos que te presentamos con algunos de los ejemplos mas fáciles de ver.




La PROPORCIÓN AUREA EN LA ARQUITECTURA
La aplicación de la Proporción Áurea en la arquitectura no es una regla estricta, sino más bien una guía estética que puede ser utilizada de diferentes maneras según el estilo arquitectónico y las preferencias del diseñador.
Algunos arquitectos optan por seguir rigurosamente la proporción áurea en todos los aspectos de su diseño, mientras que otros la utilizan de manera más sutil y adaptada a su visión creativa.
Veamos, por ejemplo, al arquitecto Le Corbusier, uno de los arquitectos más influyentes del siglo XX. Su nombre proviene de la palabra cuervo en francés que se traduce como "corbeau". Jugando con el nombre del ave y el apellido Lecorbesier de un antepasado materno, el joven suizo Charles-Édouard Jeanneret adoptó el pseudónimo de Le Corbusier.
Decía que "la belleza en la arquitectura es sinónimo de la calidad de vida de sus habitantes, es el juego sabio, correcto y magnífico de los volúmenes reunidos bajo la luz".
El planteamiento urbanístico que mostró Le Corbusier estuvo basado en la utilidad y la uniformidad, logrando una gran evolución social.
Sus obras destacan, entre otras cosas, por la proporción áurea adaptado en un esquema ideal de ergonomía llamado "Le Moduler" y su racionalismo aplicado a las partes y al todo de cada obra.
A lo largo de su producción arquitectónica, el principio de mantener la sencillez, deshacerse de toda ornamentación innecesaria y utilizar materiales prefabricados como el hormigón armado dan forma a uno de sus pilares teóricos.

Charles-Édouard JEANNERET-GRIS (1887-1965).
Arquitecto suizo nacionalizado francés en 1930. Uno de los pioneros del movimiento modernista y uno de los arquitectos más influyentes del pasado siglo. Además fue un destacado urbanista, escultor y pintor..

MODULOR
Este sistema creado por Le Corbusier se basa en las medidas de las proporciones humanas y es un canon esencial de la ergonomía moderna. Seguir sus proporciones permite tener una relación directa entre las medidas de los edificios urbanísticos y las casas o apartamentos con los individuos que en ellos transitan. La obra tuvo tanta trascendencia que hoy en día sigue siendo uno de los pilares de la arquitectura y es estudiado en todas las escuelas de arquitectura y diseño del mundo.
NOCIONES BÁSICAS DE PROYECTIVIDAD
La Real Academia de la Lengua Española define el concepto de equivalencia geométrica cómo o cuando dos figuras planas o dos sólidos con formas distintas tienen iguales respectivamente sus áreas (entendida esta como la medida de la extensión de su superficie) o sus volúmenes.
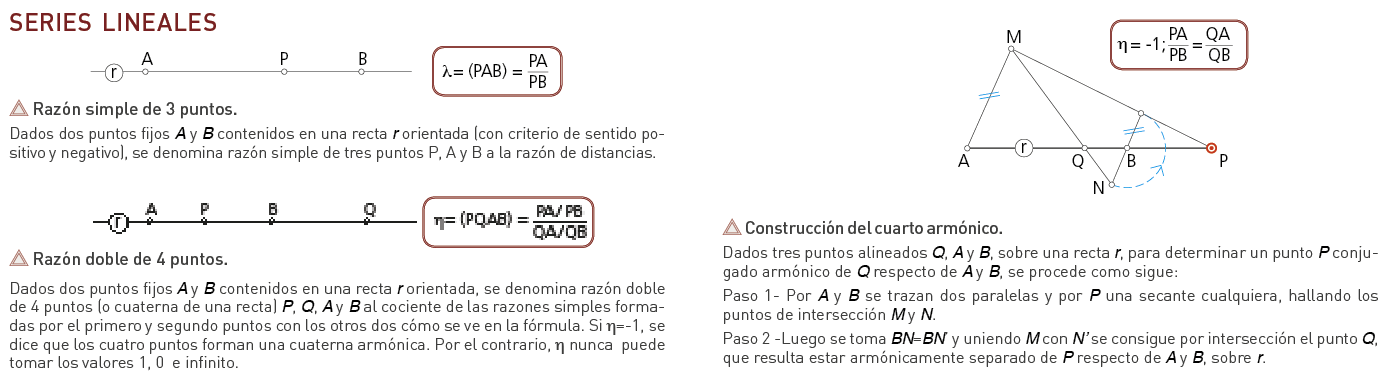
Es un concepto distinto pero intrínsecamente relacionado con los conceptos de proporción y semejanza mostrados en esta Unidad Didáctica. Para entender este concepto con mayor facilidad vamos a proponer ejemplos de equivalencia entre puntos en series lineales y en formas geométricas simples.
FORMAS GEOMÉTRICOS
Las figuras geométricas están compuestas de puntos, rectas y planos que constituyen los llamados elementos geométricos fundamentales. El movimiento rectilíneo y el movimiento coplanario de ellos da lugar a las formas geométricas, que pueden clasificarse en tres categorías.
FORMAS DE 1ª CATEGORÍA : Formas generadas al moverse un elemento geométrico.

Serie rectilinea o recta.
.
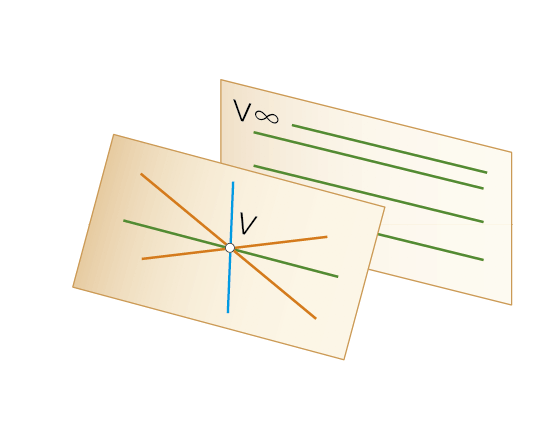
Haz de rectas coplanarias.
Tienen un punto común V, llamado vértice del haz. Se puede visualizar como el giro de una recta alrededor de V, estando siempre en el mismo plano.
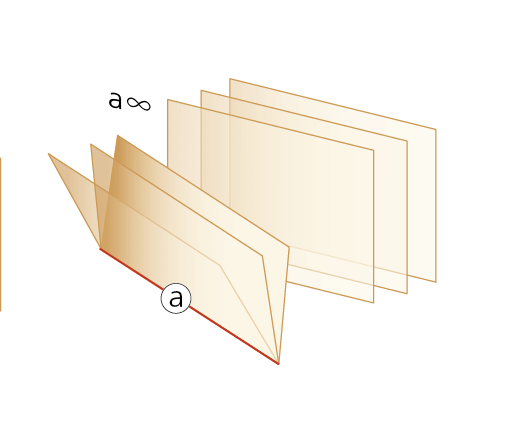
Haz de planos
Conjunto de planos que pasan por una recta llamada arista (a), pudiendo entenderse cómo el giro de un plano alrededor de una de sus rectas.
FORMAS DE 2ª CATEGORÍA Precisan dos elementos geométricos y movimiento del elemento simple.
Plano de puntos.
.
Plano de rectas.
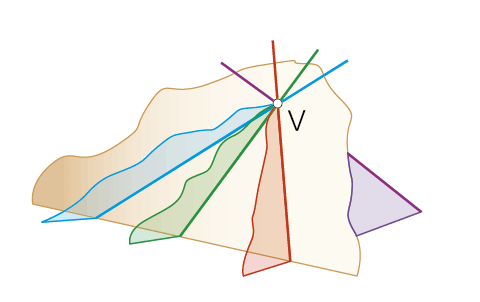
Radiación de rectas y planos.
Conjunto de las infinitas rectas y planos que pasan por un punto V (vértice o centro de radiación). A esta forma pertenecen: el haz de rectas, el de planos, las superficies cónicas y piramidales, etc
FORMAS DE 3ª CATEGORÍA
Todo conjunto de puntos, rectas y planos del espacio que no sean figuras o formas de 2ª categoría. A esta forma pertenecen los poliedros y las superficies curvas.

ESCALAS (UNE-EN ISO 5455)
Cómo ya vimos en cursos anteriores, es habitual en nuestros proyectos de arquitectura, ingeniería, diseño etc. que nos encontremos con la imposibilidad de representar gráficamente los objetos o piezas en su verdadero tamaño, ya sean diseños excesivamente grandes con relación al formato de papel, o porque al ser objetos muy pequeños no es posible dibujarlos con la debida definición gráfica. En ambos casos se ha de recurrir a reducir o ampliar proporcionalmente todas las dimensiones del objeto.
Escala es la relación entre la medida lineal representada en el dibujo y la medida lineal del objeto.
Puede venir expresada en forma de fracción, expresión decimal o como porcentaje del aumento o disminución. Así, por ejemplo, la escala 7/10 puede expresarse como 0,7 o como el 70% del natural.
Para evitar operaciones matemáticas, con escalas numéricas, se recurre al empleo de las escalas gráficas, de construcción muy sencilla cómo puedes ver en el triángulo universal de escalas que se muetra a la derecha. Este tipo de construcción te será de gran utilidad para trabajar rápidamente de forma proporcionada en tus proyectos y diseños.
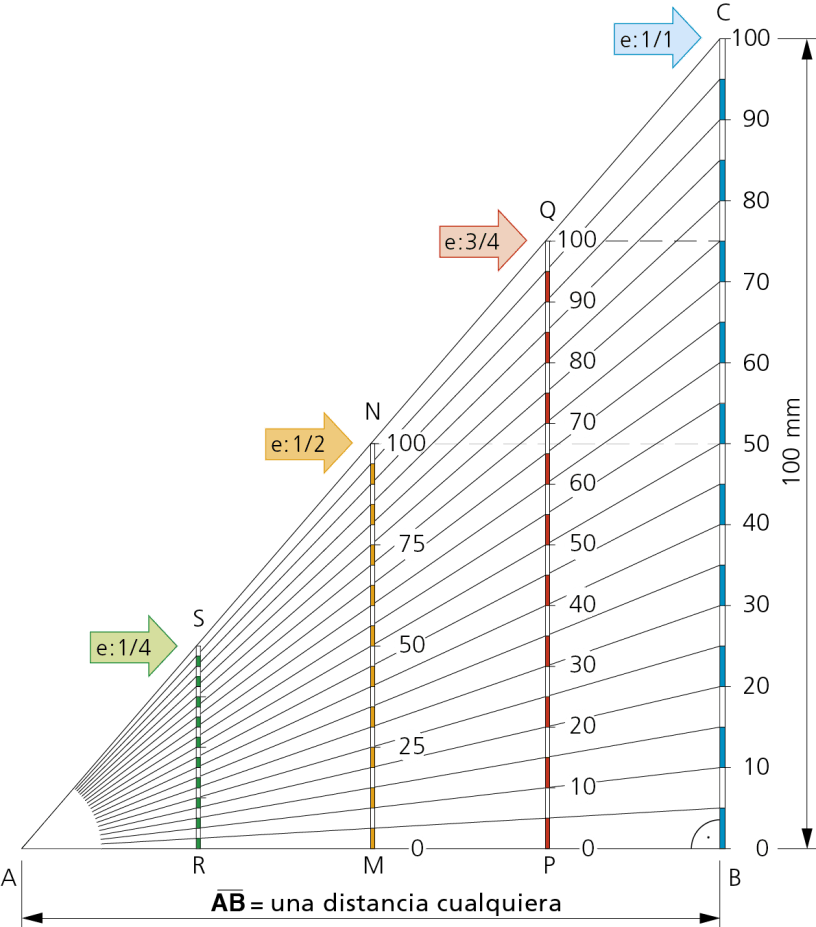
Construcción geométrica para obtener escalas de reducción y ampliación.
Se traza el triángulo rectángulo ABC, con el cateto AB de dimensión arbitraria y el otro cateto BC de 100 mm. Sobre este último, se realizan divisiones de 5 mm que se unen con A y se numeran.
- Si sobre AB se traza una perpendicular por el punto medio M, sobre ella, se obtiene la escala: e = 1/2
- Trazando otra perpendicular por P que diste 3/4 de A se obtendrá la escala:
e = 3/4
- Si se traza por R una recta perpendicular que diste 1/4 de A, se tiene la escala:
e = 1/4
Para la construcción de cualquier otra escala se procede de forma análoga.