ELEMENTOS GEOMÉTRICOS
Lugares Geométricos
Unidad 1
Los lugares geométricos se definen como el conjunto de puntos, de rectas o planos que cumplen, poseen, o se agrupan en una propiedad común.
El método de investigación de la naturaleza de un lugar geométrico (l.g.) se basa en localizar puntos que pertenezcan al lugar. La posición relativa de estos puntos indicará claramente si se trata de una recta o de una curva.
Por el momento nos ocuparemos de aquellos lugares geométricos formados por puntos y que, por su protagonismo y frecuente aparición en la estructura de las formas geométricas básicas, merecen atención prioritaria.






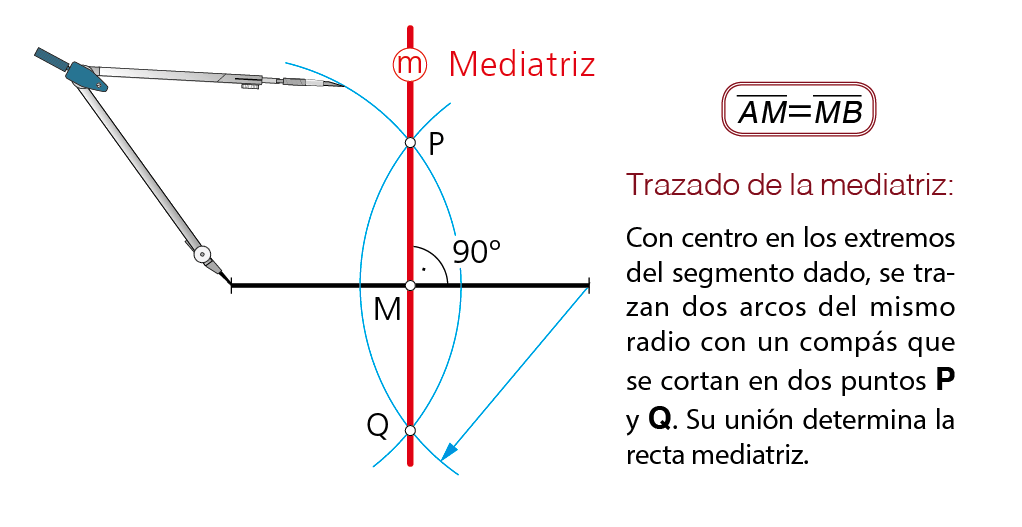
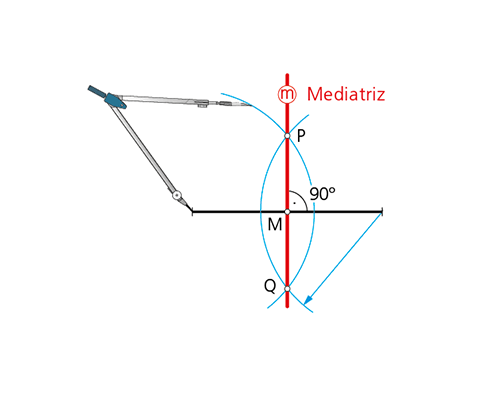
1.1 Mediatriz de un segmento.
Es el l.g. de los puntos del plano equidistantes de los extremos del segmento AB dado. Dicha mediatriz es la recta perpendicular al
segmento por su punto medio M.
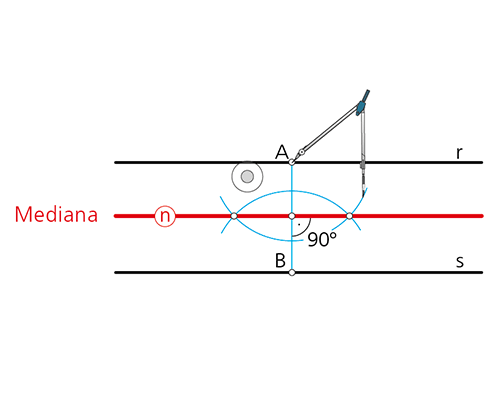
1.2 Paralela media: mediana.
El lugar geométrico de los puntos equidistantes de dos rectas paralelas es la mediatriz n del segmento que tiene por extremos los puntos A y B; es, en definitiva, la paralela media de las rectas consideradas.

En una autovía, la mediana es la línea que separa los dos sentidos de circulación.
1.3 Rectas paralelas.
El lugar geométrico de los puntos del plano equidistantes (una magnitud) de una recta m dada, son dos rectas p y q, paralelas a ella.

Hubert KIECOL (1950). «Stairs», (1994).
Escultura de cemento realizada en el estilo minimalista propio de este escultor contemporáneo. El artista usa los escalones paralelos para jugar con las luces y sombras visualmente así como la textura propia del material.
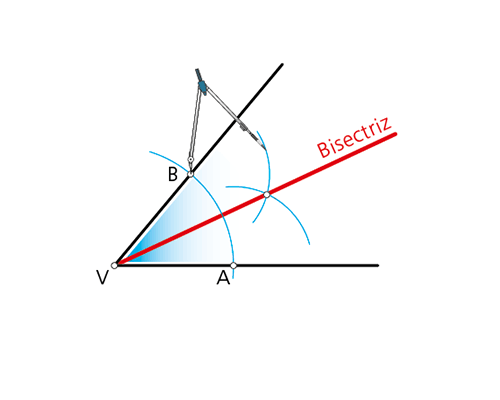
1.4 Bisectriz de un ángulo.
Es el l.g. de los puntos del plano equidistantes de los lados del ángulo.
Es la semirrecta que divide el ángulo en dos partes iguales.
Trazado si el vértice está localizado.
Con centro en el vértice V se dibuja un arco cualquiera que corta a los lados en A y B. Con centro en ellos, se trazan dos arcos, del mismo radio, consiguiendo el punto P. La unión de P con V determina la recta bisectriz.
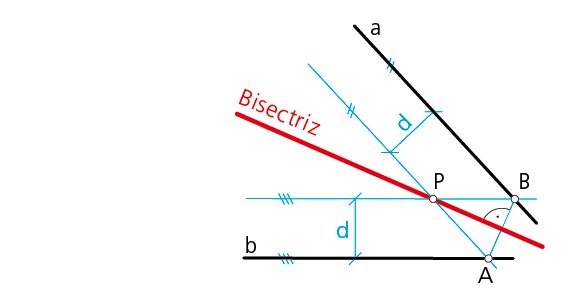
Trazado si el vértice no está localizado.
Sean las rectas a y b los lados del ángulo considerado. Se comienza por trazar dos rectas paralelas y equidistantes a dichos lados para obtener el punto de corte P. La bisectriz del ángulo queda definida al trazar por P la perpendicular al segmento AB.

1.5 Circunferencia
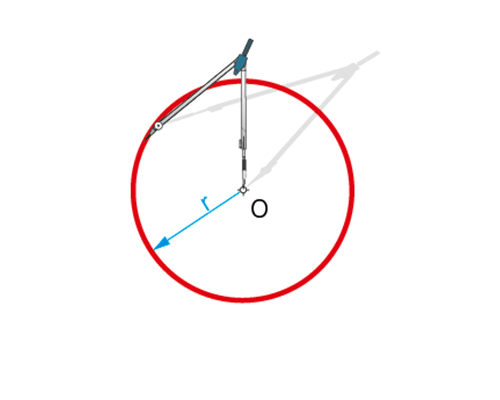
Es el lugar geométrico de los puntos del plano equidistantes (una determinada magnitud r) de un punto fijo O llamado centro.
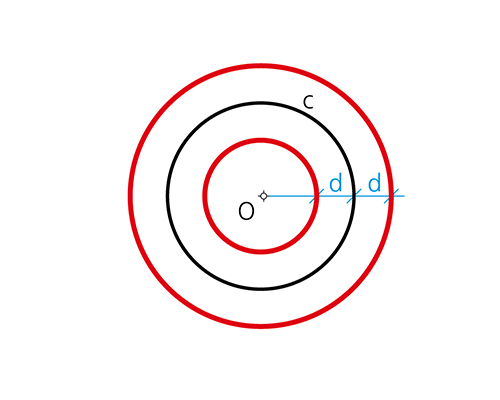
1.6 Circunferencias concéntricas
El l.g. de los puntos del plano equidistantes una magnitud d de una circunferencia c, son dos circunferencias concéntricas a esta.

Diana de dardos
Un buen ejemplo de la circunferencia concéntrica es una diana, en la cual , cuanto más nos acerquemos al centro de la misma, más puntos conseguiremos.