ELEMENTOS GEOMÉTRICOS
Ángulos en la circunferencia
Unidad 1
Según la posición del vértice de un ángulo con respecto a una circunferencia, éste puede ser: central, inscrito, semiinscrito, exterior e interior. La medida del ángulo está en función del arco o arcos que abarcan sus lados.
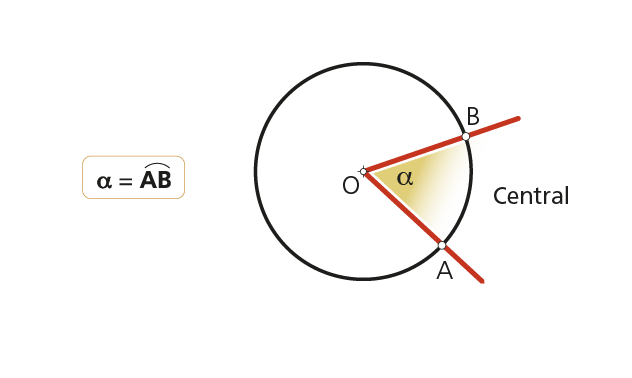
2.1 Ángulo central
Su vértice está situado en el centro de la circunferencia y sus lados son radios; y su medida la de su arco.
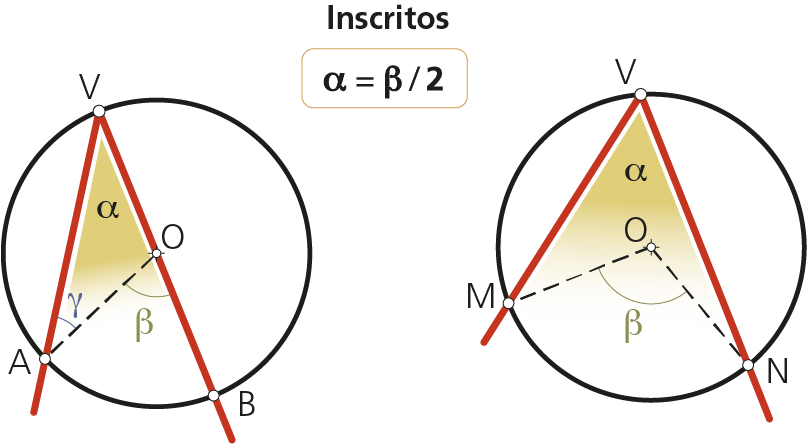
2.2 Ángulo inscrito
Su vértice está en la circunferencia y sus lados son cuerdas de la misma.
El valor del ángulo es la mitad del central cuyos lados pasan por los extremos de la cuerda. Para demostrarlo consideremos un ángulo inscrito con un lado como diámetro de la circunferencia.
En el triángulo isósceles AOV, se tiene:
α = γ; y el ángulo exterior β = α + γ = 2α por tanto: α = β/2
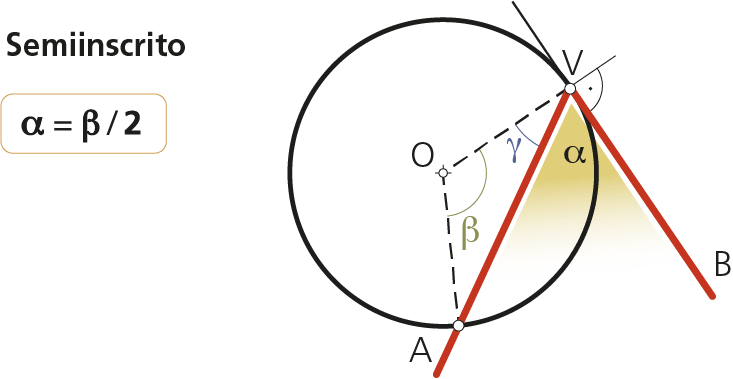
2.3 Ángulo seminscrito
Su vértice está en la circunferencia y sus lados lo forman una cuerda y una tangente.
Su valor, como en un inscrito, es la mitad del central, cuyos lados pasan por los extremos de la cuerda.
Como el ángulo OVB es recto y el triángulo AOV es isósceles, se cumple que:
α = 90°- γ = 90° - (180°- β)/2
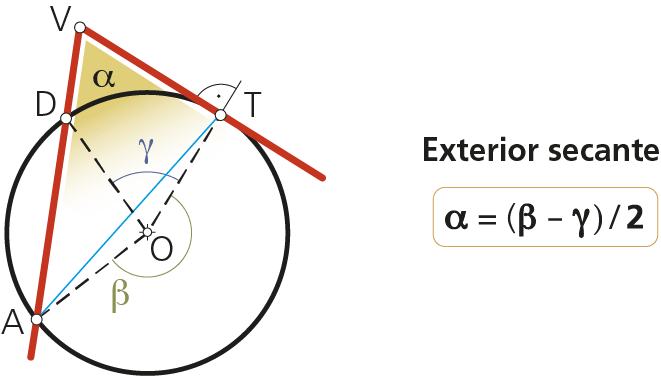
2.4 Ángulo exterior
Su vértice es exterior a la circunferencia y sus lados son secantes o tangentes a ella.
Su valor es igual a la semidiferencia de los ángulos centrales que abarcan sus lados.
2.4.1 Caso1: Cuando sus lados son secantes.
En el triángulo ACV que se forma, se cumple:
α = 180°- ángulo VAC - (180°- angulo ACB)
α = 180°- γ/2 - (180°- β/2)
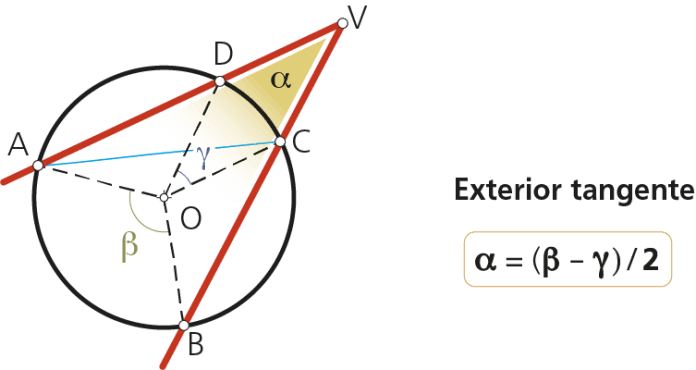
2.4.2 Caso 2: Cuando un lado es secante
En el triángulo ATV, con angulo VTA semiinscrito:
α = 180°- angulo VTA - angulo TAV
α = 180°- (180° - β/2) - γ/2
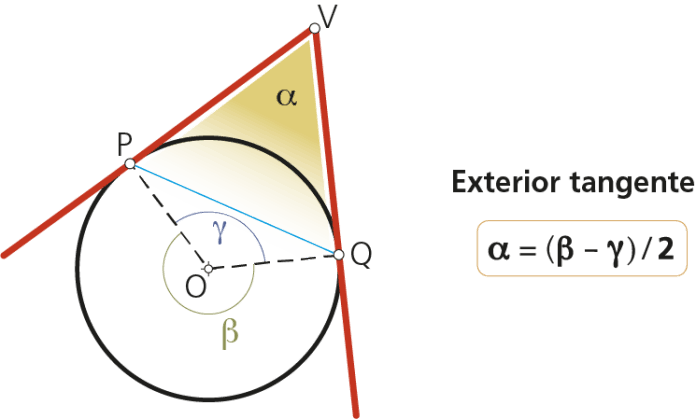
2.4.2 Caso 3: Cuando ambos son secantes
En el triángulo ATV, con angulo VTA semiinscrito:
α = 180°- angulo VTA - angulo TAV
α = 180°- (180° - β/2) - γ/2
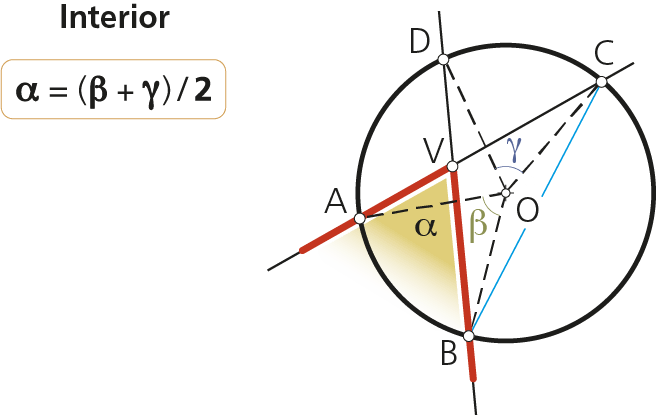
2.4 Ángulo interior
Su vértice es interior a la circunferencia.
Su valor es igual a la semisuma de los ángulos centrales que abarcan sus extremos y el ángulo opuesto por el vértice.
Considerando el triángulo BCV, se cumple:
α = 180°- ángulo BVC = 180° - (180° - ángulo VBC- ángulo VCB)
α = 180°- (180°- γ/2 - β/2);